Динамическая выпуклая оболочка (достаточно log^2 на добавление/удаление)

Эта статья находится в разработке!

Пусть дано множество точек [math]S[/math], изначально пустое, и последовательность точек [math]\{p_i\}^n_{i = 1}[/math], которые последовательно добавляются или удаляются из [math]S[/math] (естественно, точка может быть удалена, если она уже принадлежит [math]S[/math]). Требуется динамически поддерживать выпуклую оболочку [math]S[/math].

В статье описан алгоритм, требующий [math]O(\log^2{n})[/math] времени на добавление/удаление точки.

Левая и правая выпуклые оболочки

Определим левую (правую) выпуклую оболочку множества точек [math]P[/math], как выпуклую оболочку множества [math]P \cup \{\infty_+\}[/math] [math](P \cup \{\infty_-\})[/math], где [math]\infty_- = (-\infty, 0), \infty_+ = (+\infty, 0)[/math]. Тогда задачу можно свести к поддержанию отдельно левой и правой выпуклых оболочек. Далее будем рассматривать только динамическое поддержание левой оболочки (далее, для краткости, будем называть её просто выпуклой оболочкой). Заметим также, что точки вдоль выпуклой оболочки отсортированы по ординате.

Левая и правая выпуклые оболочки некоторого множества точек

Мост B между двумя выпуклыми оболочками, разделенными горизонтальной прямой

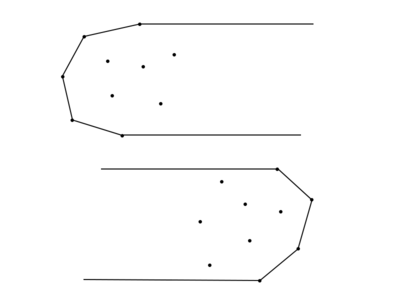
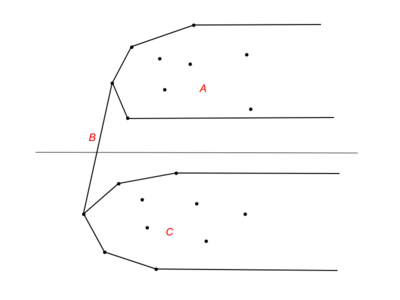
Пусть множество точек [math]P[/math] разбито горизонтальной прямой на два множества [math]A[/math] и [math]C[/math]. Рассмотрим выпуклые оболочки [math]A[/math] и [math]C[/math]. Будем называть мостом (bridge) отрезок общей касательной к этим оболочкам, заключённый между точками касания. Тогда выпуклая оболочка ко всему множеству [math]P[/math] естественным образом получается объединением частей оболочек [math]A[/math] и [math]C[/math], и моста [math]B[/math].

Основная идея алгоритма заключается в эффективном (за [math]O(\log{n})[/math]) отыскании моста, соединяющего две такие оболочки.

Структура данных

Будем хранить отсортированные лексикографически ([math]p \lt q \Leftrightarrow p_y \lt q_y \lor p_y = q_y \land p_x \lt q_x[/math]) точки в листьях сбалансированного бинарного дерева поиска (например, красно-черного или AVL). Во внутренних вершинах будем хранить вспомогательную информацию: во-первых, наименьшую точку в поддереве с корнем в данной вершине; а во-вторых, мост между выпуклыми оболочками точек левого и правого поддеревьев данной вершины. Формально вершина дерева описывается так:

struct bridge
   point left
   point right

struct node
   node    parent, left, right
   boolean leaf  // true, если лист, иначе false
   bridge  b     // поле валидно для внутренней вершины
   point   p     // если вершина лист, то точка, хранящаяся в этом листе,
                 // иначе наименьшая точка в поддереве с корнем в данной вершине

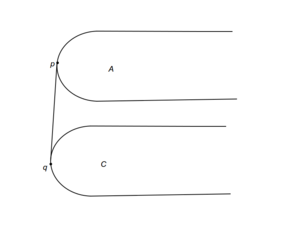
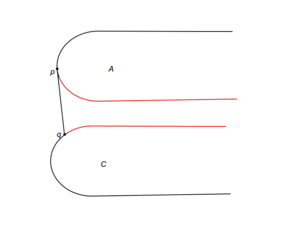
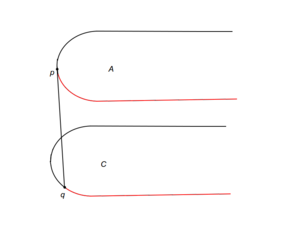
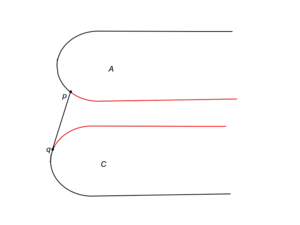
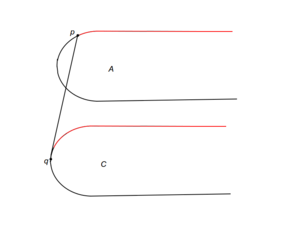
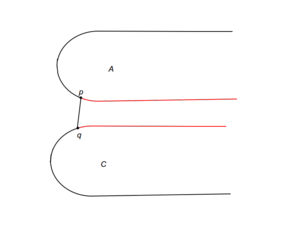
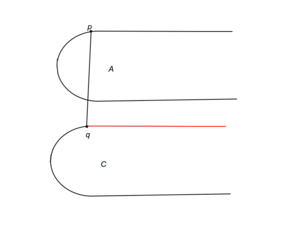
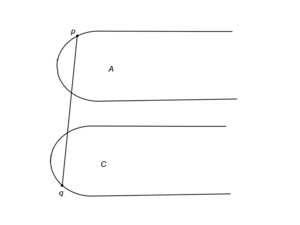
Теперь, когда отсортированные точки хранятся в структуре, поддерживающей эффективный поиск, мы можем воспользоватся идеями бинарного поиска для нахождения моста. Для этого необходим критерий спуска, по которому мы будем определять подотрезок, до которого нужно сузить задачу, имея точки [math]p[/math] и [math]q[/math], определяющие секущую к выпуклым оболочкам множеств [math]A[/math] и [math]C[/math] . В зависимости от взаимного расположения выпуклых оболочек и секущей имеем 9 случаев (a-i). Для случаев (a-h) на картинках красным показано, какие части выпуклых оболочек могут быть отброшены. Случай же i немного сложнее.

a. Касательная найдена

b. Может быть отброшена часть C после q, а также часть A перед p

c. Может быть отброшена часть C перед q, а также часть A перед p

d. По аналогии со случаем b

e. По аналогии со случаем c

f. Может быть отброшена часть C после q, а также часть A перед p

g. Только часть C после q может быть отброшена

h. По аналогии со случаем h

i. В этом случае нельзя сразу сказать, какие части A и C могут быть отброшены. Случай дробится на два

Рассмотрим подробно случай i.

Итак, на каждом шаге, мы или нашли ответ, или уменьшили размер [math]A[/math] и/или [math]C[/math] в два раза, следовательно нахождение моста работает за [math]O(\log{n})[/math].

Операции

Вставка точки

Вставим точку в дерево, как в обычное сбалансированное дерево поиска. Из-за балансировки мосты в [math]O(\log{n})[/math] вершинах дерева могут оказаться неактуальными, поэтому, возвращаясь по пути вверх до корня, будем пересчитывать мосты в таких вершинах методом, описанным выше, пользуясь тем, что всё поддерево рассматриваемой вершины уже содержит корректную информацию. Каждый пересчет моста требует [math]O(\log{n})[/math] времени, откуда итоговая асимптотика вставки: [math]O(\log^2{n})[/math].

Удаление точки

Удаление точки производится по аналогии с вставкой: сначала мы удалим точку из сбалансированного дерева поиска, а затем пересчитаем мосты, хранящиеся в вершинах, которые затронула балансировка. Очевидно, что удаление, как и вставка, работает за [math]O(\log^2{n})[/math].

Источники

• Реализация Антона Ковшарова
• Ф. Препарата, М. Шеймос. Вычислительная геометрия (1989). стр. 151 (тут описан более сложный алгоритм с двухуровневой структурой данных, но с такой же асимптотикой)
• Overmars, M. H.; van Leeuwen, J. (1981), "Maintenance of configurations in the plane" (и тут тоже)