Рёберное ядро

Определение:

Рёберное ядро (англ. core) [math]C_1(G)[/math] графа [math]G[/math] — это подграф графа [math]G[/math], порожденный объединением таких независимых множеств [math]Y \subset E(G)[/math], что [math]|Y| = \alpha_{0}(G)[/math], где [math]\alpha_{0}(G)[/math] — число вершинного покрытия.

Определение:

Вершинным покрытием (англ. vertex cover) графа [math]G[/math] называется такое множество [math]V[/math] его вершин, что у любого ребра в [math]G[/math] хотя бы одна из вершин лежит в [math]V[/math].

Определение:

числом вершинного покрытия (англ. point-covering number) называется число вершин в наименьшем вершинном покрытии графа [math]G[/math].

Критерий существования реберного ядра

Определение:

Наименьшее вершинное покрытие M графа G с множеством вершим V называется внешним (англ. external vertex cover), если для любого подмножества [math]M' \subseteq M[/math] выполняется неравнство [math]|M'| \leqslant |U(M')|[/math], где [math]U(M') = \{v| \:v \in V(G) \setminus M, \: vu \in E(G), \: u \in M'\}[/math].

Теорема:

для произвольного графа [math]G[/math] следующие утверждения эквивалентны: (1) [math]G[/math] имеет рёберное ядро. (2) [math]G[/math] имеет внешнее наименьшее вершинное покрытие. (3) каждое наименьшее вершинное покрытие для [math]G[/math] является внешним.

Доказательство:

[math]\triangleright[/math]

Обозначим минимальное вершинное покрытие [math]G[/math] как [math]M[/math]. Пусть [math]U = V(G) \setminus M[/math]. Докажем [math](1) \Rightarrow (3)[/math]. Предположим, что в [math]G[/math] существует наименьшее вершинное покрытие [math]M[/math], которое не является внешним. Это значит что [math]\exists M' : \: M' = \{u_1, \dots, u_r \}, [/math] где [math]r \leqslant \alpha_0(G)[/math], такое что [math]|M'| \gt |U(M')|.[/math] Пусть [math]U(M') = \{u_1, \dots, u_t\}, \: t \lt r[/math]. Так же, пусть [math]X[/math] — максимальное множество независимое множество ребер в [math]G[/math]. Поскольку никакие две вершины [math]U[/math] не смежны, каждое ребро из [math]X[/math] соединено, по крайней мере, с одной вершиной из [math]M[/math].

[math]\triangleleft[/math]

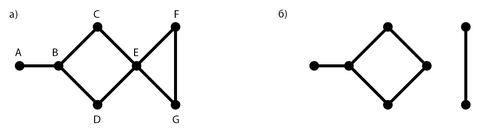
рис. 1. a) граф [math]H[/math], б) реберное ядро графа [math]H[/math]

В качестве примера рассмотрим граф H изображенный на рис. 1 а). Этот граф имеет два наименьших вершинных покрытия: [math]M_1 = \{B, E, F\}[/math] и [math]M_2 = \{B, E, G\}[/math]. Пусть [math]M_1' = M_1[/math] то [math]U(M_1') = \{A, C, D, G\}[/math]. Пусть [math]M_1'' = \{E, F\}[/math]. Тогда [math]U(M_1'') =\{C, D, G\}[/math]. Отсюда [math]|M_1'| \leqslant |U(M_1')|[/math] и [math]|M_1''| \leqslant |U(M_1'')|[/math]. И это верно для любого подмножества [math]M_1[/math]. Значит, [math]M_1[/math] — внешнее покрытие. Значит и [math]M_2[/math] — внешнее покрытие.

Реберное ядро в двудольном графе

Здесь и далее будем рассматривать двудольный граф [math]G[/math], в котором обозначим [math]S[/math] - множество вершин левой доли, [math]T[/math] - множество вершин правой доли.

Определение:

[math]G[/math] — полунесводимый граф, если [math]G[/math] имеет ровно одно вершинное покрытие [math]M[/math], такое что или [math]M \cap S[/math] или [math]M \cap T[/math] — пусто

Определение:

[math]G[/math] — несводимый граф, если он имеет ровно два наименьших вершинных покрытия [math]M_1[/math] и [math]M_2[/math], таких что либо [math]M_1 \cap S \cup M_2 \cap T = \varnothing [/math], либо [math]M_2 \cap S \cup M_1 \cap T = \varnothing[/math]

Определение:

[math]G[/math] — сводимый граф если он не является ни полунесводимым, ни сводимым.

Теорема:

[math]G[/math] и его реберное ядро [math]C_1(G)[/math] совпадают тогда и только тогда, когда [math]G[/math] является двудольным и не является сводимым.