Пусть [math]G(V, E)[/math] — двусвязный кубический граф.
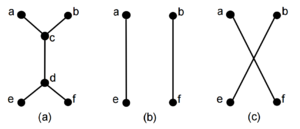
Возьмём ребро [math]p = (c, d)[/math]. Пусть вершины [math]a[/math] и [math]b[/math] смежены с вершиной [math]c[/math], а вершины [math]e[/math] и [math]f[/math] смежны с вершиной [math]d[/math] (рисунок [math]1 (a)[/math]).
Как минимум одно из двух сокращений графа [math]G[/math], состоящее из удаления вершин [math]c, d[/math] и пересоединения вершин [math]a, b, e, f[/math] рёбрами [math](a, e), (b, f)[/math] или [math](a, f), (b, e)[/math] (рисунок [math]1 (b), (c)[/math]) сохранит двусвязность графа. |
|
Обозначим компоненты графа [math]G(V - {c, d})[/math] как [math]A, B, E, F[/math], которые содержат вершины [math]a, b, e, f[/math] соответственно. Так как [math]G[/math] не имеет мостов (соответственно [math]p[/math] не является мостом) должно существовать ребро, соединяющее одну из компонент [math]A[/math] или [math]B[/math], с одной из компонент [math]E[/math] или [math]F[/math]. Без потери общности предположим, что [math]A[/math] соединено с [math]E[/math]. Заметим, что рёбра [math](b, c), (d, f)[/math] так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок [math]3[/math]):
- компонента [math]B[/math] соединена с [math]F[/math]
- компонента [math]B[/math] соединена с [math]E[/math] и компонента [math]E[/math] соединена с [math]F[/math]
- компонента [math]A[/math] соединена с [math]B[/math] и компонента [math]E[/math] соединена с [math]F[/math]
Во всех трёх случаях если [math]G(V - {c, d})[/math] расширить рёбрами [math](a, f), (b, e)[/math] (получим граф [math]G'[/math]), добавленные рёбра будут лежать на некотором цикле в [math]G'[/math] (рисунок [math]4[/math]). Так же, для любой пары вершин [math]u, v[/math] [math]\in[/math] [math]{a, b, e, f}[/math] существует цикл в [math]G'[/math], содержащий данные вершины. Чтобы доказать, что [math]G'[/math] двусвязен, нужно показать, что каждое ребро [math]r[/math] из [math]G'[/math] лежит на некотором цикле в [math]G'[/math]. Пусть цикл [math]C[/math] в [math]G[/math] содержит [math]r[/math] (такой цикл существует, так как [math]G[/math] двусвязен). Если [math]C[/math] не проходит через вершины [math]c, d[/math] тогда [math]C[/math] так же является циклом в [math]G'[/math], иначе построим цикл [math]C'[/math] графа [math]G'[/math] из [math]C[/math] следующим образом:
- если путь [math] x - c - d - y [/math] [math]\in[/math] [math] C [/math], [math] x [/math] [math]\in[/math] [math] \{a, b\} [/math], [math] y [/math] [math]\in[/math] [math] \{e, f\} [/math], удалим этот путь и добавим любой другой из [math] x [/math] в [math] y [/math] в [math] G' [/math], не содержащий [math]r[/math] (такой путь всегда существует, так как [math] x [/math] и [math] y [/math] принадлежат некоторому циклу в [math] G' [/math]),
- если путь [math] a - c - b [/math] [math]\in[/math] [math] C [/math], удалим этот путь и добавим любой другой из [math] a [/math] в [math] b [/math] в [math] G' [/math], не содержащий [math]r[/math],
- если путь [math] e - d - f [/math] [math]\in[/math] [math] C [/math], удалим этот путь и добавим любой другой из [math] e [/math] в [math] f [/math] в [math] G' [/math], не содержащий [math]r[/math].
|