Дерево палиндромов

Дерево палиндромов — структура данных, позволяющая решить некоторые интересные задачи на палиндромы.

Эту структуру данных придумал Михаил Рубинчик и рассказал ее на летних сборах в Петрозаводске в 2014 году.

Описание структуры

Дерево палиндромов состоит из вершин. Каждая вершина соответствует палиндрому. Через [math]u.value[/math] будем обозначать строку, которой соответствует вершина [math]u[/math].

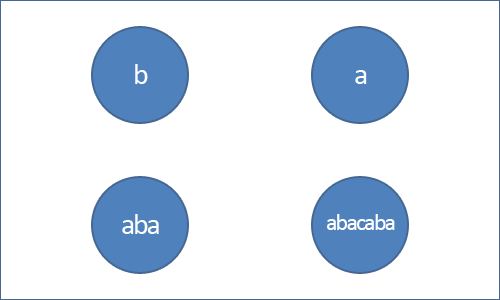
Ребра дерева палиндромов ориентированные и помечены символами. Ребро с символом [math]x[/math] из вершины [math]u[/math] в вершину [math]v[/math] означает, что [math]v.value=x+u.value+x[/math]. Тут [math]``+""[/math] означает конкатенацию строк.

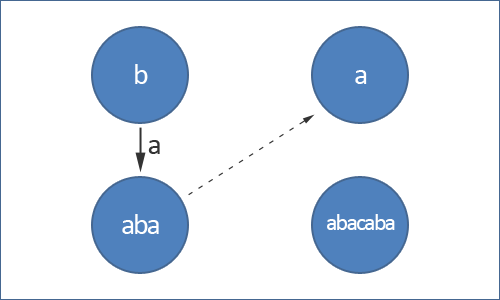
Также в дереве палиндромов присутствуют суффиксные ссылки. Суффиксная ссылка из вершины [math]u[/math] ведет в вершину [math]w[/math], если [math]w.value[/math] является наибольшим суффиксом строки [math]u.value[/math].

Реализация

Название структуры данных выбрано не совсем удачно, т.к. на самом деле она представляет из себя два дерева, однако суффиксные ссылки могут вести как в то же, так и в другое дерево. Это сделано для удобства реализации. Также в целях экономии памяти мы будем хранить для каждой вершины не строки, а позицию в исходной строке ([math]u.pos[/math]) и размер палиндрома ([math]u.len[/math]).

Итак, у нас будет два дерева. Одно дерево для палиндромов четной длины, другое {---} для палиндромов нечетной длины. Каждое дерево будет иметь фиктивный корень. Обозначим корни четного и нечетного дерева соответственно [math]root_{even}[/math] и [math]root_{odd}[/math].

[math]root_{odd}[/math] будет соответствовать фиктивному палиндрому длины -1. Это нужно для того, чтобы не обрабатывать отдельно случай добавления палиндрома длины 1. Теперь каждый раз при добавлении новой вершины [math]u[/math] к вершине [math]v[/math] мы будем просто указывать ее длину равной [math]u.len = v.len + 2[/math].

Источники

• Palindromic tree