Алгоритм Бржозовского

Задача:

Пусть дан автомат [math]\mathcal{A}[/math]. Требуется построить автомат [math]\mathcal{A}_{min}[/math] с наименьшим количеством состояний, распознающий тот же язык, что и [math]\mathcal{A}[/math].

Описание

Пусть [math]q[/math] — состояние автомата [math]\mathcal{A} = \langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to Q \rangle[/math].

Определение:

Правым языком (англ. right language) — называется язык [math]L_d(q)[/math], принимаемый автоматом [math]\mathcal{A}_{d}(q) = \langle \Sigma , Q , q , T , \delta \rangle[/math], полученным из [math]\mathcal{A}[/math] путём добавления уникального начального состояния [math]q[/math].

Определение:

Левым языком (англ. left language) — называется язык [math]L_g(q)[/math], принимаемый автоматом [math]\mathcal{A}_{g}(q) = \langle \Sigma , Q , q , T , \delta \rangle[/math], полученным из [math]\mathcal{A}[/math] путём добавления уникального терминального состояния [math]q[/math].

Утверждение (1):

Автомат является детерминированным тогда и только тогда, когда левые языки его состояний попарно не пересекаются.

Определение:

Обратное слово [math]r(u)[/math] для слова [math]u[/math] определяется следующим образом: [math]r(\varepsilon) = \varepsilon[/math] и если [math]u = u_1 u_2 u_3 \dotsc u_p[/math], тогда [math]r(u) = v_1 v_2 v_3 \dotsc v_p[/math], где [math]v_i = u_{p - i + 1}[/math].

Определение:

Обратный язык для языка [math]L[/math] — язык [math]r(L) = \{ u \mid r(u) \in L \}[/math].

Определение:

Обратный автомат для автомата [math]\mathcal{A} = \langle \Sigma , Q , S , T , \delta \rangle[/math] — автомат [math]r(\mathcal{A}) = \langle \Sigma , Q , T , I , r(\delta) \rangle[/math], полученный из [math]\mathcal{A}[/math] сменой местами начальных и конечных состояний и сменой направлений переходов.

Утверждение (2):

Если [math]\mathcal{A}[/math] распознает язык [math]L[/math], то [math]r(\mathcal{A})[/math] распознает [math]r(L)[/math].

Утверждение (3):

Если левый язык состояния [math]q[/math] в [math]\mathcal{A}[/math] — [math]L_g(q)[/math], тогда его левый язык в [math]r(A)[/math] — [math]L_d(q)[/math]. Аналогично для правого языка [math]q[/math].

Пусть [math]\mathcal{A} = \langle \Sigma , Q , I , T , \delta \rangle[/math] — НКА.
Тогда детерминированный автомат [math]d(\mathcal{A}) = \langle \Sigma , Q' , \{ i' \} , T' , \delta' \rangle[/math] определяется следующим образом:

• Детерминированному состоянию соответствует множество недетерминированных состояний: для каждого [math]q' \in Q'[/math] имеем [math]q' \subseteq Q[/math],
• Начальное состояние в [math]d(\mathcal{A})[/math] — множество из [math]I[/math] начальных состояний автомата [math]\mathcal{A}[/math],
• Состояние в детерминированном автомате является терминальным тогда и только тогда, когда оно содержится хотя бы в одном недетерминированном состоянии,
• Пусть [math]q'[/math] — состояние детерминированного автомата и [math]a[/math] – символ из [math]\Sigma[/math]. Если переход из [math]q'[/math] по символу [math]a[/math] определен, тогда, по построению: [math]\delta'(q', a) = \bigcup\limits_{q \in q'}{ \delta(q, a)}[/math].

Утверждение (4):

Правый язык состояния [math]q'[/math] [math]d(\mathcal{A})[/math] эквивалентен объединению правых языков состояний [math]q[/math] автомата [math]\mathcal{A}[/math], принадлежащих множеству [math]q'[/math].

Определение:

Левое отношение регулярного языка [math]L[/math] для слова [math]u[/math] из [math]\Sigma^{*}[/math] — язык [math]u^{-1}L = \{ v \in X^{*} \mid uv \in L \}[/math].

Минимальный автомат [math]\mathcal{A}_{L}[/math] для регулярного языка [math]L[/math] определяется следующим образом:

• множество состояний — это множество левых отношений языка [math]L[/math],
• начальное состояние — [math]L[/math],
• терминальные состояния — множество отношений, содержащих пустое слово,
• функция перехода [math]\delta(u^{-1}L, x) = (ux)^{-1}L[/math].

Автомат [math]\mathcal{A}_L[/math] уникален с точностью до изоморфизма и имеет минимальное количество состояний.

Утверждение (5):

Детерминированный полный достижимый автомат минимален тогда и только тогда, когда правые языки его состояний различны.

Алгоритм

Описание

Алгоритм минимизации конечных автоматов Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:

• Он элегантен и весьма оригинален.
• Он эффективен.
• Он работает даже с недетерминированными конечными автоматами.

Пусть [math]\mathcal{A}[/math] — конечный автомат. [math]d(\mathcal{A})[/math] — детерминизированный автомат для [math]\mathcal{A}[/math], [math]r(\mathcal{A})[/math] — обратный автомат для [math]\mathcal{A}[/math].
Обозначим [math]d(r(\mathcal{A}))[/math] как [math]dr(\mathcal{A})[/math], [math]r(d(r(\mathcal{A})))[/math] как [math]rdr(\mathcal{A})[/math], [math]d(r(d(r(\mathcal{A}))))[/math] как [math]drdr(\mathcal{A})[/math].

Теорема (Бржозовский, 1962):

Пусть [math]\mathcal{A}[/math] — автомат (необязательно детерминированный), распознающий язык [math]L[/math]. Минимальный детерминированный автомат [math]\mathcal{A}_L[/math] может быть вычислен следующим образом: [math]\mathcal{A}_L = drdr(\mathcal{A})[/math].

Доказательство:

[math]\triangleright[/math]

По построению автомат drdr(A) конечный. Согласно утверждению 2, он распознает язык L. Покажем, что правые языки drdr(A) все различны. Из утверждения 1, левые языки dr(A) попарно не пересекаются. Из утверждения 3, правые языки rdr(A) являются левыми языками dr(A). Таким образом, они попарно не пересекаются. Согласно утверждению 4, правый язык drdr(A) – объединение правых языков rdr(A). Поскольку правые языки rdr(A) попарно не пересекаются, все правые языки drdr(A) различны. Тогда, согласно утверждению 5 автомат drdr(A) минимальный.

[math]\triangleleft[/math]

Пример работы

1. Исходный НКА ([math]FA[/math]):
   
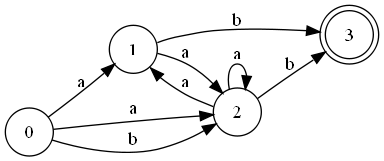
2. Первый шаг алгоритма ([math]\operatorname{rev}(FA)[/math]):
   
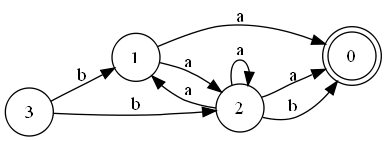
3. Второй шаг алгоритма ([math]\operatorname{det}(\operatorname{rev}(FA))[/math]):
   
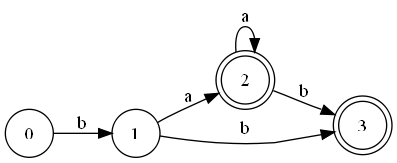
   [math]\operatorname{det}[/math] переименовывает состояния, после этого [math]0[/math] всегда является начальным состоянием
4. Третий шаг алгоритма ([math]\operatorname{rev}(\operatorname{det}(\operatorname{rev}(FA)))[/math]):
   
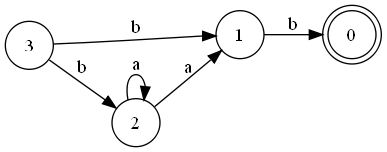
   После выполнения этого шага алгоритма оба состояния [math]2[/math] и [math]3[/math] являются начальными.
5. Заключительный шаг алгоритма ([math]\operatorname{det}(\operatorname{rev}(\operatorname{det}(\operatorname{rev}(FA))))[/math]):
   

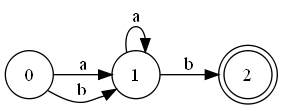
Заключение

Самым эффективным алгоритмом минимизации принято считать алгоритм Хопкрофта, который, как и прочие традиционные алгоритмы, работает только с ДКА. Его асимптотическое время выполнения зависит от логарифма исходных данных. С другой стороны очевидно, что алгоритм Бржозовского в худшем случае будет обладать экспоненциальным временем выполнения, ведь этого требует процедура детерминизации, выполняемая дважды. На практике же наблюдается парадокс, алгоритм Бржозовского во многих случаях опережает прочие подходы к минимизации, включая и алгоритм Хопкрофта. В работе, сравнивающей оба алгоритма, показано, что алгоритм Бржозовского оказывается эффективнее алгоритма Хопкрофта для автоматов с большим числом переходов.

См. также

• Минимизация ДКА, алгоритм за O(n^2) с построением пар различимых состояний
• Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))

Источники информации

• Алгоритм Бржозовского для минимизации конечного автомата