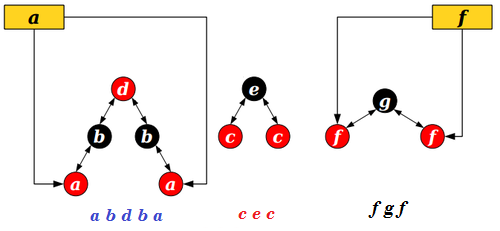
Деревья Эйлерова обхода
Содержание
Задача о динамической связности
| Задача: |
Для динамически изменяющегося дерева выполнить следующие запросы:
|
Для решения поставленной задачи будем представлять дерево в виде его эйлерова графа, а затем будем работать с эйлеровым обходом (англ.Euler tour tree) этого графа. Это позволит выполнять указанные запросы за .
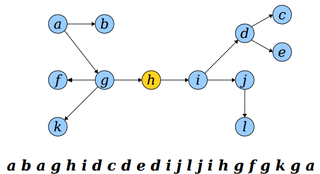
Представление деревьев в виде эйлерова графа
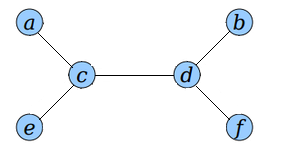
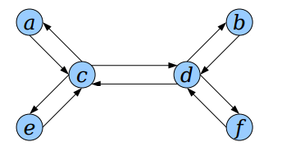
Для представления дерева в виде эйлерового графа заменим каждое ребро дерева на два ребра и .
Получившийся ориентированный граф будет эйлеровым согласно критерию.
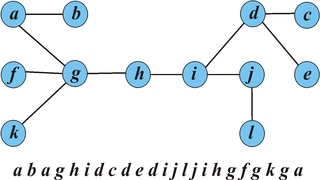
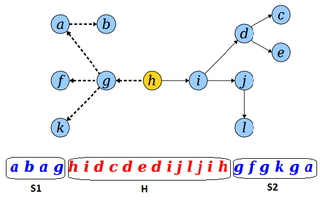
Представим дерево с корнем в вершине в виде последовательности вершин, посещеннных в порядке эйлерова обхода.
| Утверждение: |
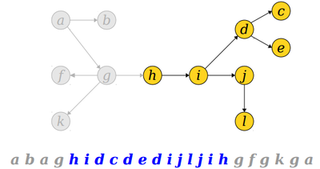
Последовательность вершин между первым и последним вхождениями вершины в эйлеров обход дерева, представляет эйлеров обход поддерва с корнем в . |
|
Действительно, при обходе дерева последний раз выйдем из вершины, только после посещения всех вершин ее поддерева. |
Операции c эйлеровыми обходами
Представление деревьев в виде их эйлеровых обходов позволяет свести задачу о динамической связности к следующим операциям с последовательностями вершин:
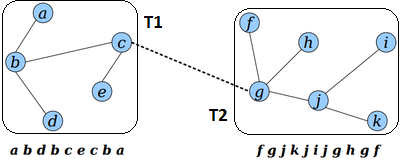
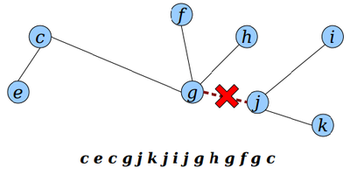
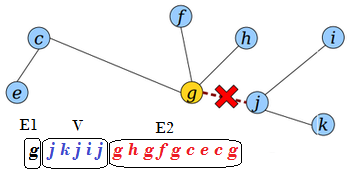
Изменение корня дерева (переподвешивание)
Дано дерево с корнем в вершине . Требуется переподвесить его к вершине .
Для переподвешивания (англ. rerooting) необходимо:
- Разбить эйлеров обход на три части:
- - вершины, посещенные эйлеровым обходом до захода в .
- - вершины между первым и последним вхождением нового корня .
- - вершины, посещенные эйлеровым обходом после выхода из .
- Удалить первую вершину в .
- Соединить в следующем порядке: , , .
- Добавить в конец последовательности.
В результате получим:
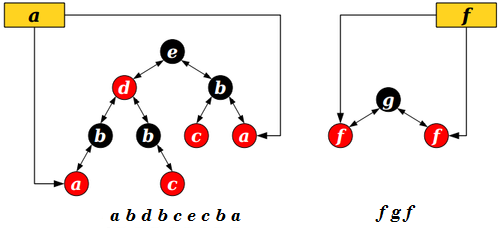
Добавление ребра
Для связывания деревьев и , где , а добавлением ребра необходимо:
- Переподвесить дерево к вершине , если корнем дерева была другая вершина.
- Переподвесить дерево к вершине , если корнем дерева была другая вершина.
- Соединить получившиеся эйлеровы обходы.
- Добавить в конец последовательности.
В результате получим эйлеров обход дерева с корнем в вершине :
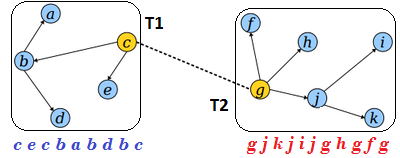
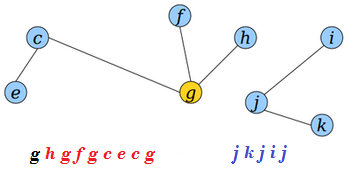
Разрезание ребра
Для разбиения дерева на два поддерева путем разрезания ребра необходимо:
- Переподвесить дерево к вершине .
- Разделить дерево на части , где отрезок между первым и последним вхождением вершины .
- Эйлеров обход первого поддерева образуется соединением и , с удалением повторного в месте их соединения.
- Эйлеров обход второго поддерева образует .
В результате получим:
Реализация структуры
Представим последовательность вершин эйлерова обхода в виде сбалансированного двоичного дерева. Будем использовать красно-черное дерево.
Объединение и разделение красно-черных деревьев выполняется за .
Для каждой вершины храним указатели на её первое и последнее вхождение в последовательность. Значит, имеем доступ к ним за .
Запрос о принадлежности вершин к одной компоненте связности выполняется за проверкой лежат ли эти вершины в одном дереве.
См. также
Примечания