Обсуждение участницы:Анна
Содержание
Примеры доказательств
Язык
| Определение: |
| Определим как множество первых половин цепочек языка , то есть множество существует , для которой , причем . |
Например, если , то . Заметим, что цепочки нечетной длины не влияют на .
| Утверждение: |
Пусть — регулярный язык. Тогда язык также регулярен. |
|
Так как — регулярный язык, то существует ДКА , допускающий его. Рассмотрим строку . Для того, чтобы проверить, что , нам надо убедиться, что существует строка такой же длины, что и , которая, будучи сконкатенированной с , даст строку из , то есть если на вход автомату подать , то в конце обработки мы окажемся в терминальном состоянии. Предположим, что автомат, закончив обработку , находится в состоянии , то есть . Мы должны проверить, что существует строка которая ведет из состояния до какого-нибудь терминального состояния , то есть . |
Язык
| Определение: |
| Определим как множество цепочку можно представить в виде , где . |
Например, если , то .
| Утверждение: |
Пусть — регулярный язык. Тогда язык также регулярен. |
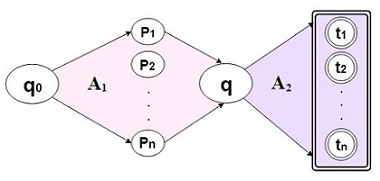
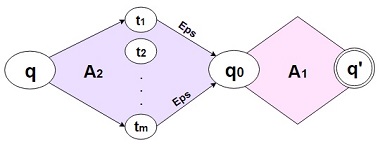
| Так как — регулярный язык, то существует допускающий его ДКА . Построим из недетерминированный автомат с переходами следующим образом: рассмотрим состояние , из которого есть переходы в другие состояния (то есть начиная с можно построить непустое слово, заканчивающееся в терминальной вершине). Тогда если какое-то слово проходит через это состояние, оно может быть зациклено таким образом, что его суффикс, начинающийся с , станет префиксом нового слова, а префикс, заканчивающийся в — суффиксом. Разделим автомат на две части и такие, что будет содержать все вершины, из которых достижима , а — все вершины, которые достижимы из (см. рис. 1). Заметим, что каждая вершина может содержаться в обеих частях одновременно, такое может случиться, если автомат содержит циклы. Теперь перестроим автомат так, что он будет принимать слова "зацикленные" вокруг , то есть начинающиеся с и после достижения терминальной вершины продолжающиеся с (см. рис. 2). Для этого стартовой вершиной сделаем и построим от нее часть . Теперь добавим состояние и соединим с ним все терминальные состояния из с помощью переходов. Далее построим от часть . Добавим вершину , эквивалентную , и сделаем ее терминальной. Данный автомат принимает слова, зацикленные вокруг выбранной вершины . Мы хотим, чтобы автомат принимал слова, зацикленные вокруг любой такой . Для этого создадим новую стартовую вершину и свяжем ее переходами со всеми перестроенными автоматами (зацикленными вокруг всех подходящих ), в том числе и с изначальным автоматом. Построенный автомат допускает язык , следовательно, данный язык является регулярным. |
Для лучшего понимания алгоритма перестроения автомата рассмотрим пример.
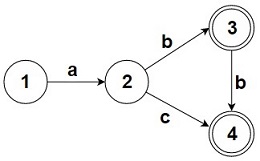
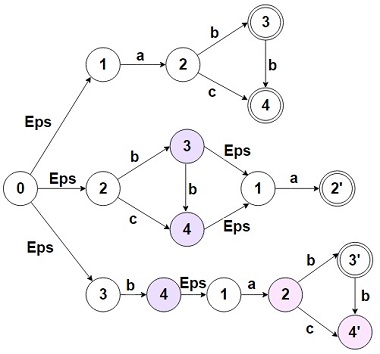
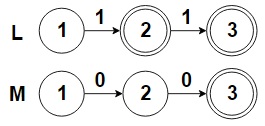
На рис. 3 представлен автомат, допускающий язык . На рис. 4 показано, как этот автомат был перестроен. Были добавлены части, зацикленные относительно вершин и . Появилась новая стартовая вершина , которая связана переходами с изначальным автоматом и его измененными версиями. Данный автомат распознает язык : первые три слова распознает первая часть, которая совпадает с изначальным автоматом; следующие три — вторая, перестроенная относительно вершины ; последнее слово распознает третья часть, зацикленная относительно вершины .
Язык
| Определение: |
| Пусть и . Определим . Распространим это определение на языки следующим образом: пусть и — два языка над одним алфавитом . Тогда . |
Например, если и , то .
| Утверждение: |
Пусть и — регулярные языки. Тогда также является регулярным. |
|
Так как и — регулярные языки, то существуют ДКА , распознающий язык , и , распознающий язык . Построим автомат , который будет распознавать язык . Идея следующая: каждое состояние этого автомата будем описывать тремя значениями , где , и . Нам нужно организовать чередование переходов по состояниям автоматов, то есть если мы на определенном шаге перешли от одного состояния автомата до другого, то на следующем мы обязаны совершить переход по состояниям автомата . Для этого нам нужно обновлять состояние одного автомата и при этом сохранять состояние другого для следующего перехода. Тут мы будем использовать третье значение: если , то будет двигаться по состояниям первого автомата, то есть значение при переходе в новое состояние автомата поменяется, останется неизменной, станет , если , то, соответственно, все наоборот. То есть у нас будут две функции перехода, выбирать нужную будем в зависимости от четности третьего параметра. Важно, что на каждом шаге мы инвертируем значение , что гарантирует чередование. Определим автомат следующим образом:
|
Чтобы более наглядно показать, как строится автомат , разберем пример. Пусть и (см. рис. 5). Все состояния нового автомата представлены на рис. 6. Стартовая вершина , множество терминальных вершин — .