Гиперграфы
| Определение: |
| Гиперграфом называют такую пару , где - множество вершин, а - семейство подмножеств X, называемых гиперребрами |
Гиперграф, у которого арность гиперребрер равна двум( т.е. каждое гиперребро содержит только две вершины), является графом.
Основные понятия гиперграфов
Пусть - подмножество . Множество частичных гиперребер, индуцированных множеством вершин в , называется
называется вершинно-порожденным множеством. С этого момента, будем рассматривать сокращенные гиперграфы(т.е. никакое гиперребро не содержится в другом).
Рассмотрим множество . Подгиперграфом гиперграфа , индуцированного множеством вершин , наызывается такой гиперграф с множеством гиперребер , которое является множеством частичных гиперребер, индуцированных множеством вершин в .
Путем между двумя гиперребрами и гиперграфа называется последовательность гиперребер , таких что :
1) и
2)
Гиперграф называется связным тогда и только тогда, когда существует путь между каждой парой гиперребер.
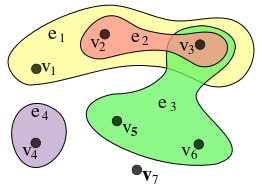
Пусть - связный, сокращенный набор гиперребер, и - элементы и . называется сочленением , если его удаления из всех гиперребер разрывает это множество. На рис.1 является сочленением .
Гиперграф называется - ацикличным, если каждое множество частичных ребер является связными, сокращенным, индуцированным множеством вершин и не допускающее сочленения, является тривиальным(т.е. содержит только один элемент).
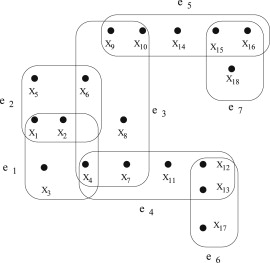
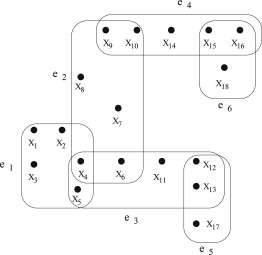
Гиперграф на рис.1 не является - ацикличным, так как множество частичных гиперребер является связным, уменьшенным, не тривиальным и не допускают сочленения. Напротив, гиперграф на рис.2 является - ацикличным.
Пусть дан гиперграф . Циклом в называется последовательность гиперребер удовлетворяющим следующим свойствам:
и , где