PS-полнота задачи Generalized geography

Формулировка задачи

Рис. 1. Граф для игры в города в штате Мичиган

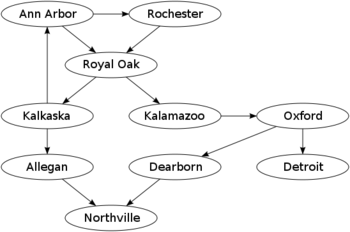
Города (Geography) - игра, в которой игроки по очереди называют города со всего мира. Каждый город должен начинаться с той буквы, на которую заканчивается предыдущий, повторы запрещены. Игра начинается с любого города, и заканчивается, когда игрок проигрывает и не может назвать новый город.

Графическая модель

Для визуализации задачи можно построить ориентированный граф, где каждая вершина - имя города, а ориентированное ребро из А в Б означает, что город Б начинается на ту же букву, на которую заканчивается город А. Ход игрока - переход из текущей вершины в новую, ранее не посещенную, по соответствующему ребру. Проигрывает тот, кто не может сделать ни одного перехода (см. рис. 1).

Рис. 2. Пример графа для игры в Generalized Geography

В игре Generalized Geography (Обобщенные города) мы заменяем граф с городами на некоторый абстрактный ориентированный граф. Игроки по очереди переходят из вершины в вершину, и проигрывает тот, кто не может сделать новый ход (перейти в ранее не посещенную вершину).

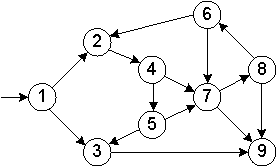
Рассмотрим пример (рис. 2). Пусть P1 - игрок, который ходит первым, и P2 - игрок, который ходит вторым. Игра начинается с первой вершины. Здесь игрок P1 обладает следующей выигрышной стратегией: делает ход в вершину 2, после чего P2 переходит в вершину 4, так как это единственный вариант. Первый игрок ходит в вершину 5, и второй выбирает между вершинами 3 и 7. Но независимо от выбора игрока P2, P1 может перейти в вершину 9, откуда второй игрок никуда не может пойти.

Утверждение

Язык [math] GG = \{ \langle G, b \rangle | [/math] первый игрок в графе [math] G [/math], начиная игру с вершины [math] b [/math], обладает выигрышной стратегией [math] \} [/math] является PS-полным.

Доказательство

Доказательство принадлежности задачи классу PS

Чтобы показать, что язык принадлежит классу PS, предъявим алгоритм, работающий на полиномиальной памяти, определяющий, обладает ли игрок выигрышной стратегией находясь в вершине v графа G.

Алгоритм [math] M ( \langle G, b \rangle ) [/math] :

1. Если из вершины, в которой находится игрок, не ведет ни одного ребра в непосещенные ранее вершины, то вернем FALSE, мы проиграли.

2. Иначе запустим этот же алгоритм от всех вершин, в которые можно пойти, и если везде вернется TRUE, вернем FALSE, куда бы мы ни пошли, второй игрок выиграет. Если же хоть из одной вершины функция вернула FALSE, то вернем TRUE, в этой вершине второй игрок проигрывает.

Этот алгоритм перебором находит выигрышную стратегию для первого игрока, и очевидно, требует полиномиальную память: на каждом шаге одна или более вершин помечаются как посещенные, и более не обрабатываются.

Доказательство принадлежности задачи классу PSH

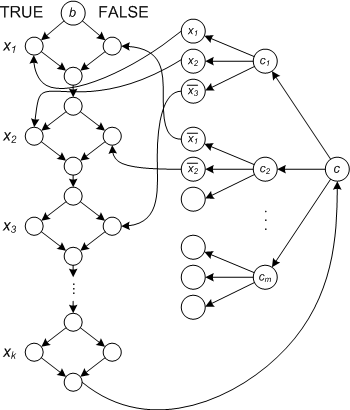
Для доказательства этого факта сведем задачу о выполнимости булевой КНФ-формулы с предваряющими кванторами (эта задача PS-трудная) к Generalized Geography за полиномиальное время. Для этого рассмотрим задачу о выполнимости КНФ-формулы с предваряющими кванторами как игру двух игроков [math] \exists [/math] и [math] \forall [/math].

Если в нашей формуле с предваряющими кванторами последний квантор - не [math] \exists [/math], то добавим его, введя дополнительную переменную. Таким образом для игры двух игроков [math] \exists [/math] и [math] \forall [/math] наша формула представима в следующем виде: [math] \varphi = \exists x_1 \forall x_2 \exists x_3 ... \exists x_n ( \psi ) [/math] , где [math] \psi [/math] - некая КНФ-формула.

Рис. 3. Модель графа для сведения задачи об игре двух игроков [math] \exists [/math] и [math] \forall [/math] к задаче GG

Для любой такой КНФ-формулы с предваряющими кванторами можно построить граф, аналогичный приведенному на рисунке 3. Рассмотрим этот граф, и докажем, что это сведение задачи об игре игроков [math] \exists [/math] и [math] \forall [/math] к задаче Generalized Geography.

Левый столбец в этом графе описывает процедуру выборки игроками [math] \exists [/math] и [math] \forall [/math] значений переменных, если игрок выбирает TRUE, он идет в левую сторону, иначе в правую.

Зафиксировав значения переменных, игрок [math] \forall [/math] (т.к. в нашей КНФ-формуле с предваряющими кванторами последний квантор [math] \exists [/math]) выбирает скобку, значение которой должно быть FALSE (тогда он выиграет!). На рисунке каждая скобка - отдельная вершина [math] c_i [/math].

После того, как игрок [math] \forall [/math] зафиксировал скобку, игрок [math] \exists [/math] долджен выбрать переменную, значение которой не ноль (игроки уже зафиксировали значения переменных в самом начале) и сделать переход в соответсвующую вершинку. Т.к. значение этой переменной не ноль, то игрок [math] \forall [/math] не сможет никуда пойти из этой вершины (тогда [math] \exists [/math] выиграл, первый игрок обладает выигрышной стратегией в игре Generalized Geography). Для этого проведем ребра из каждый скобки [math] c_i [/math] в вершины-переменные, учавствующие в этой скобке, а от них проведем ребра к вершинам левого столбца, соответсвующим выборам TRUE или FALSE значений переменных.

Таким образом, если игрок [math] \exists [/math] выигрывает, то автоматически обладает выигрышной стратегией и первый игрок в Generalized Geography. Он знает, какие значения переменных надо выбрать, и в какую вершину пойти в конце. Аналогично, по выигрышной стратегии первого игрока в Generalized Geography можно узнать, какие значения переменных должен выбрать игрок [math] \exists [/math] для того, чтобы удовлетворить формулу.

Мы свели задачу об игре игроков [math] \exists [/math] и [math] \forall [/math] к задаче Generalized Geography. Очевидно, сведение будет произведено за полиномиальное время. Значит, язык [math] GG [/math] является PS-трудным, а так как выше мы доказали его принадлежность классу PS, то и PS-полным.