Проблема четырёх красок
| Теорема (Проблема четырех красок): |
Теорема о четырёх красках — утверждение о том, что всякую карту можно раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета. Под общим участком границы понимается часть линии, то есть стыки нескольких областей в одной точке общей границей для них не считаются. |
Общие идеи доказательства
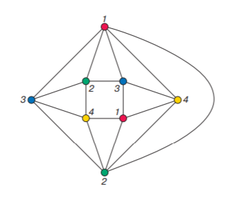
Начнем с того, что заменим задачу раскраски плоской карты на эквивалентную ей проблему. Выберем столицу у каждой страны и соединим дугами столицы стран, имеющих общий сегмент границы. В результате получится планарный граф. Тогда следующая теорема эквивалентна теореме выше:
| Теорема (Хроматическое число планарного графа): |
Хроматическое число планарного графа не превосходит . |
В таком виде в году проблема четырех красок была доказана К. Аппелем и У. Хакеном. Значительную часть проверок выполнил компьютер, из-за чего доказательство было принято не всеми математиками. Само доказательство имеет невероятные размеры, и из-за его сложности мы не сможем рассмотреть его целиком, но посмотрим на общие идеи, которые в нем используются.
Во-первых, если грани образованные нашим планарным графом не триангуляция (то есть имеют не ровно три ребра у их границ), мы можем добавлять ребра без внедрения новых вершин до тех пор, пока все грани не станут триангулированными. Если полученный граф является раскрашиваемым в не более чем цвета, то и исходный граф раскрашиваем так же (так как удаление ребер не увеличивает хроматическое число). Поэтому достаточно доказать теорему для триангулированных графов, и без потери общности мы предполагаем, что граф триангулирован.
Для дальнейших рассуждений нам понадобится следующее утверждение:
| Утверждение: |
Для триангулированного графа , где — количество вершин степени , а — максимальная степень вершины в графе. |
| Так как граф триангулирован, то , где — количество ребер, а — количество граней. Из формулы Эйлера |
Из данного утверждения следует, что в графе существует вершина степени не больше .
Попытаемся доказать теорему от противного. Пусть у нас существует граф, который требует хотя бы цветов для раскраски. Среди всех таких графов существует минимальный, то есть такой граф , что удаление любой вершины из него делает его -раскрашиваемым.
| Утверждение: |
В : |
| Если в есть вершина степени , то мы можем просто удалить ее из графа, раскрасить полученный граф в цвета, вернуть удаленную вершину и покрасить ее в один из цветов, не занятых соседями. Аналогично теореме Хивуда доказывается, что удалив вершину степени также всегда можно раскрасить граф в цвета. |
Для вершины степени аналогичное утверждение неверно, хотя оно и присутствовало в одном из первых ошибочных доказательств.
На этом этапе мы натыкаемся на самую сложную часть доказательства. Имея дело со случаем вершины степени , нельзя просто удалить ее. Тогда вместо вершины будем рассматривать связанный подграф из нескольких вершин (назовем его конфигурацией). Сводимыми назовем такие конфигурации, что если при их удалении граф -раскрашиваемый, то его окраска может быть изменена таким образом, что при возвращении конфигурации граф также можно раскрасить в цвета. Например, конфигурация состоящая из вершины степени не больше является сводимой (было доказано выше). Неизбежной конфигурацией назовем такое множество конфигураций, что хотя бы одна из конфигураций этого множества обязана быть в нашем графе.
Если нам удастся найти какую-то неизбежную конфигурацию и доказать, что с ней граф все равно -раскрашиваем, доказательство будет завершено. Основным методом для нахождения такого набора является метод разгрузки.
Приведем пример нахождения неизбежной конфигурации:
| Утверждение: |
В планарном графе есть вершина степени не больше или конфигурация, состоящая из вершин степени или из вершины степени и степени |
| Присвоим каждой вершине некую величину — груз . Предположим что наше утверждение неверно. Следовательно, в графе нет вершин степени не больше . Тогда положительный груз есть только у вершин степени (и он равен единице). У вершин степени груз , а у всех остальных он отрицательный. По первому доказанному выше утверждению мы знаем, что сумма грузов по всем вершинам . Значит вершины степени должны компенсировать все отрицательные грузы других вершин. Пусть каждая такая вершина отдает по своего груза соседям. Тогда у всех вершин степени и груз останется равен (помним что вершины степени не смежны с вершинами степени по предположению). Рассмотрим все остальные вершины. Так как мы проводим доказательство для триангулированных графов, то у вершины степени не может быть больше чем соседей степени . Однако для , следовательно, сумма грузов отрицательна. Получено противоречие. |
Выше мы получили неизбежную конфигурацию, состоящую из небольшого количество элементов. Подобными действиями Аппель и Хакен провели операций разгрузки и получили неизбежную конфигурацию из конфигураций. Некоторые из них являются сводимыми, доказательством раскрашиваемости графов с остальными и занимался компьютер.