Дерево решений и случайный лес
Версия от 19:34, 20 января 2019; 91.215.122.38 (обсуждение)
Содержание
Дерево решений
| Определение: |
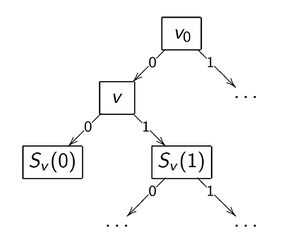
Дерево решений (англ. decision tree, DT) — алгоритм классификации , задающийся деревом (связным ациклическим графом):
|
| Определение: |
Бинарное дерево решений — частный случай дерева решений, для которого .
|
Y classify(x): while : ((x)) ; return
Рекурсивный алгоритм построения бинарного дерева решений ID3
Идея алгоритма (англ. Induction of Decision Tree) заключается в последовательном дроблении выборки на две части до тех пор, пока в каждой части не окажутся объекты только одного класса. Проще всего записать этот алгоритм в виде рекурсивной процедуры , которая строит дерево по заданной подвыборке и возвращает его корневую вершину.
V ID3(): if все объекты множества принадлежат одному классу then создать новый лист return v найти предикат с максимальной информативностью: Gain(, ) разбить выборку на две части по предикату : if или then создать новый лист = класс, в котором находится большинство объектов из else создать новую внутреннюю вершину = ID3() = ID3() return
Мера неопределенности распределения
Критерий ветвления
Критейрий Джини
Энтропийный критерий
Критерии останова
Рекурсию останавливают в следующих случаях:
- Все объекты множества принадлежат одному классу , тогда создается лист с меткой класса
Деревья регрессии
Критерии ветвления
Рецукция решающих деревьев
Оценивание вероятностей
Полужадный синтез
Алгоритмы построения решающих деревьев
Обобщающая способность решающих деревьев
Композиции решающих деревьев
- Решающий лес
- Бустинг над решающими деревьями
История
Ссылки
- Classification and Regression Trees — лекции Cosma Shalizi, ноябрь 2009.