Представление функции класса DM с помощью медианы
Задача из ДЗ №2. Доказать, что любую монотонную самодвойственную функцию(self-Dual, Monotone), можно представить с использованием медианы(majority function, median operator).
Для n = 1, удовлетворяют DM .
Для n = 2, удовлетворяют DM .
Для n = 3, удовлетворяют DM и собственно медиана. .
Теперь рассмотрим произвольную монотонную самодвойственную функцию для n > 3. Обозначим аргументы за , то есть . Тогда введем три функции от n - 1 аргумента:
Очевидно, они также самодвойственны и монотонны из определения f, и f можно выразить одной из функций , так как 2 из 3 аргументов точно совпадут. Теперь выразим f через :
Докажем, что это так. Для удобства обозначений пусть . Тогда есть несколько случаев:
- . Очевидно, выполняется.
- . Тогда:
- Получили 2 случая:
-
- Тогда можно упорядочить по возрастанию наборов их переменных(используя свойство их монотонности):
- . Так как - между остальными, то оно и будет медианой .
- . Доказывается аналогично.
- - симметричный случай.
- - симметричный случай.
Все!
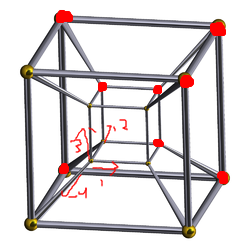
P.S. У меня такое чувство, что классу DM принадлежат только проекторы и их комбинации(точнее, дизъюнкция попарных конъюнкций). Если представить вектора значений аргументов в виде n - мерного куба, то если функция на всех его гранях, содержащих вершину , будет равна 1, то на противоположной грани, везде будет 0. Это для проекторов. А дизъюнкция попарных конъюнкций проекторов - попарные пересечения граней, то есть все ребра n-мерного куба, содержащие вершину . Такая функция также будет самодвойственной и монотонной. Не знаю только как более математически это обосновать.
Не, это немного гон, хотя проекторы действительно такие.
Внезапно, количество таких функций при каждом n.