Индексация данных. Упорядоченные и хеш-индексы

Индексы

Индексы нужны для того, чтобы оптимально искать нужные записи в таблице.

Всего есть два способа найти нужные данные:

• Полный просмотр таблицы
  • Последовательный перебор записей
  • Быстро работает на маленьких таблицах, но медленно на средних и больших
  • Если выбираем большую часть данных, то работает быстро. Иначе - медленно
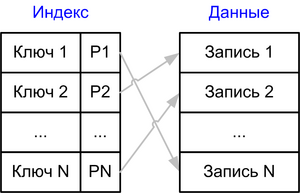
• Индекс
  • Произвольный набор столбцов
  • Требуется предварительная обработка таблицы как при построении, так и при обновлении
  • Быстрый поиск в индексе, сразу получаем указатель на запись

Кластеризованный индекс

Кластеризованный индекс

Если данные в таблице хранятся в порядке индекса, то такой индекс называется кластеризованным. Кластеризованный индекс позволяет увеличить скорость просмотра, однако так хранить данные возможно только если в таблице есть всего один индекс.

Структура Индекса

Структура индекса

В общем случае индексы хранят отображение из ключей на идентификаторы записей, которые ведут на записи, которые мы загружаем

Есть два подхода к реализации индексов:

• Хеш-таблицы
• Деревья поиска

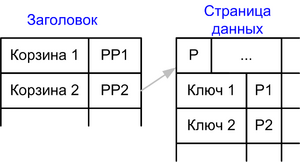
Хеш-индексы

• Предварительная обработка
  • Подсчет хешей ключей. Хеш-функция задается разработчиком СУБД, что дает нам гарантии хорошего статистического распределения.
  • Разбиение на корзины
• Поиск в индексе
  • Просмотр корзины
  • Несколько ключей в корзине. Коллизии могут быть, так как индекс не всегда ключ.
• Заголовок помещяется в памяти

Простой хеш-индекс

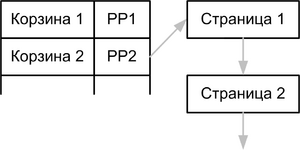
Однако может наступить момент, когда очередная корзина не помещается в страницу, в таком случае мы так же храним их цепочками.

• Так как хеш-функция хорошая, то в цепочке только полезные данные
• Если цепочка длинная, значит этому набору столбцов соответствует много строк, значит база данных так и задумывалась.

При этом получаем

• Линейное время поиска
• В случае, если данных много, мы не можем просто увеличить число корзин и перенести данные, так как перехешировать таблицу очень долго

Цепочки страниц

Расширяемое хеширование

• Большое количество корзин, сильно больше чем требуется
• Несколько корзин на одной странице, чтобы не аллоцировать для каждой корзины страницу
  • Обычно - последовательных
  • Разделение корзин при переполнении страницы
• Не работает при плохой хеш-функции, но у нас хорошая

При переполнении страницы мы:

• разделяем ее на несколько страниц
• разделим страницы, которые на нее ссылались, на несколько групп
• Каждой такой группе выделим по странице

Стоимость - 1 чтение и запись стольких страниц, на сколько мы разделили (обычно 2)

Расширяемое хеширование

Побитное расширяемое хеширование

• Глубина хеша $n$
  • Создадим $2^n$ корзин
• Для каждой страницы хранится ее локальная глубина $k$
  • Это значит что она хранит $2^{n−k} последовательных корзин на странице
  • Может быть разной для разных страниц
• При переполнении происходит разделение корзин
  • Страница глубины $k$ разделяется на две глубины $k+1$

Ускоряемые запросы

• Проверка существования ключа
  • Проверка повторений (ключи)
  • in - только если есть все необходимые атрибуты
  • exist - только если есть все необходимые атрибуты
  • count - зачастую можно посчитать по индексу count, не обращаясь к самим записям
• Поиск по ключу
  • Естественные соединения

Упорядоченные индексы

Традиционно реализуются на деревьях поиска

• Предварительная обработка
  • Ключи упорядочиваются по возрастанию - так как ключ составной, то используем лексикографисечкое возрастание
• Поиск в индексе
  • Поиск в упорядоченной последовательности

Деревья поиска

• Количество операций
  • Обычно пропорционально $O$(высоты)
  • Минимизировать высоту
• Размер узла
  • Хотим эффективно использовать страницы
  • Сильно ветвящиеся деревья, так размер узла будет ~странице и высота будет минимальной

$B$ и $B+$ деревья

• $B$ деревья степени $n$
  • От $\frac{n}{2}$ до n детей
  • Указатели и ключи хранятся в узлах
• $B+$ деревья степени $n$
  • От $\frac{n}{2}$ до $n$ детей
  • Указатели хранятся в листьях

• $B+$ меньше данных в узлах - сильнее ветвятся
• $B+$ на одну страницу глубже

Мы храним корень и несколько первых уровней в памяти для быстрого обращения, из-за этого время работы может резко возрастать, когда заканчивается закешированные уровни.

Плотные и разряженные индексы

• Плотный индекс
  • Храним ключи всех элементов
• Разряженные индекс
  • Храним ключи части элементов
  • Обычно – один на страницу, мы можем найти данные в рамках этой страницы без загрузки новых
  • Разряженный индекс бычно используется для кластеризованных индексов
  • Уменьшает число уровней

Так как упорядоченных индекс хранит сами данные в узлах, а не только хеш, то чем больше индексируеммые данные, тем меньше степень ветвления

• Строки
  • Много данных в ключе – меньше степень ветвления
  • Можно использовать префиксы

Строки опасно использовать в качестве индекса, может сильно вырости высота дерева

• Суррогатные ключи
  • Малый размер
  • Выше эффективность

Широкие и низкие деревья - хорошо

• Изменяющиеся данные
  • Частое обновление индекса
  • Уменьшение индекса

Не эффективно, для уменьшения данных нужна отдельная таска

Ускоряемые запросы

• Проверка существования ключа
• Поиск по ключу
• Минимум и максимум среди значений, на которых построен ключ
• Диапазон
  • Загрузка
  • count. count * работает быстроее, так как не нужно идти по всем данным
• Если построен на строках, like по префиксу

Литература

• Дейт К. Введение в системы баз данных (Приложение Г)
• Кнут Д. Искусство программирования. Том 3. Сортировка и поиск
• Silberschatz A., Korth H. F., Sudarshan S. Database System Concepts