Этапы обработки запроса. Перезапись запросов
В этом разделе будут рассмотрен этап обработки запросов, а именно перезапись запросов
Содержание
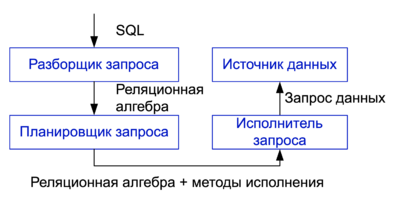
Обработка запроса
Мотивирующий пример
Пусть есть следующая база данных:
- Students(SId, FirstName, LastName, GId, Year)
- $10^4$ записей
- Индексы: (SId) (кластеризованный), (GId)
- Groups(GId, Name)
- $10^3$ записей
- Индексы: (GId) (кластеризованный), (Name)
И следующий запрос:
Фамилии студентов группы M3439
select LastName from Students natural join Groups where Name = 'M34391'
Планы запросов без индексов
- План 1
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G)))$
- $10^4·10^3 + 10^4·10^3 + 10^4 + 20 ≈ 2·10^7$ операций
- План 2
- $π_{Name}(σ_{Name=M34391}(S ⋈ G))$
- $10^4·10^3 + 10^4 + 20 ≈ 10^7$ операция
- План 3
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + 10^4 + 20 ≈ 10^4$ операций
Планы запросов с индексами
- План 4. Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $10^3 + (3 + 20) + 20 ≈ 10^3$ операций
- План 5. Groups(Name), Students(GId)
- $π_{Name}(S ⋈ σ_{Name=M34391}(G))$
- $2 + (3 + 20) + 20 ≈ 45$ операций
От выбора плана сильно зависит производительность
Наиболее медленный план $2·10^7$ операций
Наиболее быстрый план $45$ операций
Обработка запроса
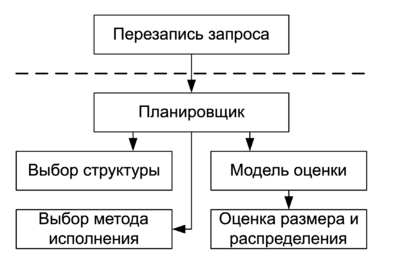
Перезапись и планировщик
- Перезапись запроса
- Статические правила оптимизации запроса
- Считается, что полезны всегда
- Планировщик запроса
- Оптимизация в зависимости от данных
- Перебор вариантов
Выбор структуры и метода
- Выбор структуры
- Преобразование запроса
- Порядок выполнения операций
- Порядок соединений
- Выбор метода исполнения
- Как исполняется каждая операция
Оценка плана
- Модель стоимости
- Стоимость операции
- Размер операндов
- Размер результата
- Оценка размера и распределения
- Статистика по данным
- Статистика предыдущих запросов
Перезапись запроса
Минимизация набора операций
Преобразование подзапросов
- Преобразуются в реляционную алгебру
- Запись в реляционном исчислении
- Вынос кванторов
- Преобразование в алгебру
Преобразование соединений
- Внешние соединения
- $R_1 \ojoin_θ R_2 ⇒ (R_1 \ljoin_θ R_2) ∪ (R_1 \rjoin_θ R_2)$
- $R_1 \ljoin_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_1 - π_{R_1}(σ_θ(R_1 × R_2)))$
- $R_1 \rjoin_θ R_2 ⇒ σ_θ(R_1 × R_2) ∪ (R_2 - π_{R_2}(σ_θ(R_1 × R_2)))$
- Декартово соединение
- $R_1 × R_2 ⇒ R_1 ⋈ R_2$
Унарные операции
Повторная фильтрация
- Правило
- Повторное применение фильтрации заменяется одинарным
- $σ_{cond_1}(σ_{cond_2}(R)) ⇒ σ_{cond_1 ∧ cond_2}(R)$
- Пример
- $π_{FirstName}(σ_{Name=M34391}(σ_{S.GId=G.GId}(S × G))) ⇒ π_{FirstName}(σ_{Name=M34391 ∧ S.GId=G.GId}(S × G))$
Повторная проекция
- Правило
- Повторное применение проекции заменяется внешней
- $π_{A}(π_{B}(R)) ⇒ π_{A}(R)$
- Пример
- $π_{FirstName}(π_{FirstName, Name}(S × G)) ⇒ π_{FirstName}(S × G)$
Проекция и фильтрация
- Правило
- Фильтрация осуществляется до проекции
- $σ_{cond}(π_{A}(R)) ⇒ π_{A}(σ_{cond}(R))$
- Пример
- $π_{FirstName}(σ_{Name=M34391}(π_{FirstName, Name}(S × G))) ⇒ $
- $π_{FirstName}(π_{FirstName, Name}(σ_{Name=M34391}(S × G))) ⇒ $
- $π_{FirstName}(σ_{Name=M34391}(S × G))$
Алгебраические свойства операций
Дистрибутивность операций
- Фильтрация
- $σ_{cond}(R_1 ∪ R_2) ⇒ σ_{cond}(R_1) ∪ σ_{cond}(R_2)$
- $σ_{cond}(R_1 \cap R_2) ⇒ σ_{cond}(R_1) \cap σ_{cond}(R_2)$
- $σ_{cond}(R_1 - R_2) ⇒ σ_{cond}(R_1) - σ_{cond}(R_2)$
- $σ_{cond_1 ∧ cond_2}(R_1 ⋈ R_2) ⇒ σ_{cond_1}(R_1) ⋈ σ_{cond_2}(R_2)$
- Проекция
- $π_A(R_1 ∪ R_2) ⇒ π_A(R_1) ∪ π_A(R_2)$
- $π_A(R_1 ∩ R_2) ⇏ π_A(R_1) ∩ π_A(R_2)$
- $π_A(R_1 - R_2) ⇏ π_A(R_1) - π_A(R_2)$
- $π_{A}(R_1 ⋈ R_2) ⇒ π_A(π_{(A ∪ R_2) ∩ R_1}(R_1) ⋈ π_{(A ∪ R_1) ∩ R_2}(R_2))$
Коммутативность операций
Коммутативные операции
$⋈$, $∪$, $∩$
Некоммутативные операции
$-$
$\div$, $\gdiv$
Применение коммутативности
Выбор левой и правой стороны для несимметричных методов исполнения
Ассоциативность операций
Ассоциативные операции
$⋈$, $∪$, $∩$
Неассоциативные операции
$-$
$\div$, $\gdiv$
Применение ассоциативности
Выбор порядка выполнения операций
Обработка условий
Замыкание предикатов
- Примеры правил
- $a = b ∧ b = c ⇒ a = b ∧ b = c ∧ a = c$
- $a > b ∧ b = c ⇒ a > b ∧ b = c ∧ a > c$
- $a > b ∧ b > c ⇒ a > b ∧ b > c ∧ a > c$
- Пример
- $σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒$
- $σ_{P_1.p > P_2.p ∧ P_2.p ≥ 60 ∧ P_1.p > 60}(P_1 ⋈_{P_1.SId = P_2.SId} P_2) ⇒$
- $σ_{P_1.p > P_2.p}(σ_{p > 60}(P_1) ⋈_{P_1.SId = P_2.SId} σ_{p ≥ 60}(P_2))$
КНФ и ДНФ
Преобразование предикатов
Конъюнктивная нормальная форма
Дизъюнктивная нормальная форма
Вычисление КНФ
Слева направо, до первой лжи
Вычисление ДНФ
Слева направо, до первой истины
Семантические оптимизации
Семантическая оптимизация
Применение знания об ограничениях
Неэквивалентные запросы
Тот же результат
Пример
$π_{FirstName}(Students ⋈ Groups) ⇒ π_{FirstName}(Students)$, если $Students.GId ⊂ Groups.GId$
Пример оптимизации
Ограничение
У всех, кто получает стипендию все оценки ≥60
check not HasScolarship or 60 <= all (select Points from Points where Points.SId = Id)
Запрос
Оценки стипендиатов группы M34391 по СУБД
select Points from Students natural join Points where HasScolarship and CId = 10 and GId = M34391
$σ_{HasScolarship ∧ CId = 10}(Students ⋈ Points)$
Оптимизированный запрос
$σ_{GId=M34391 ∧ HasScolarship}(Students) ⋈⋈ σ_{60 ≥ Points ∧ CId = 10}(Points)$