Многомерное дерево отрезков

Дерево отрезков можно обобщить в многомерный случай для решения таких задач, как поиск суммы на прямоугольнике (или гиперпрямоугольной области).

Задача:

Рассматривается задача регионального поиска. Задано множество точек в [math]p[/math]-мерном евклидовом пространстве. Образцом для поиска является гиперпрямоугольная область. Найти сумму/минимум/максимум.

Построение

Пусть задано [math]p[/math]-мерное пространство с координатными осями [math]x_1, x_2, x_3...x_p[/math]. Т.к. при построении одномерного дерева, индексы массива разбиваются на отрезки, тогда при построении многомерного дерева координаты будут обрабатываться сначала по [math]x_1 [/math], затем по [math]x_2[/math] и так далее... Далее дерево строится рекурсивно: далее координаты по [math]x_1[/math] обрабатываем по координатам [math]x_2[/math], [math]x_3[/math] (по всем возможным координатам) и далее по аналогии... То есть получается, что основная идея построения многомерного дерева отрезков - вкладывание деревьев отрезка друг в друга.

Пример задачи, в которой удобно использовать многомерное дерево отрезков

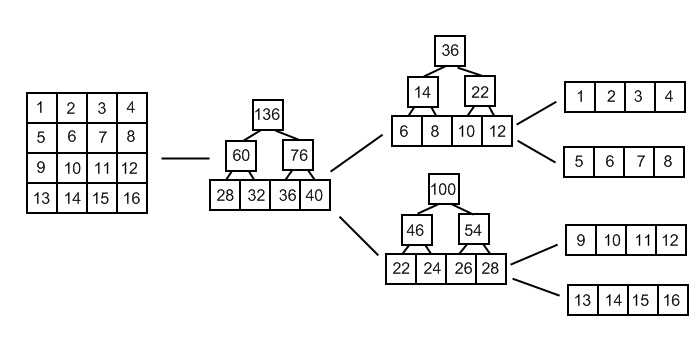
Пример двумерного дерева

Рассмотрим процесс построения предельного случая при [math]p = 2[/math]. Пусть задан массив элементов размера [math]n \times m[/math]. Упорядочим массив по первой координате и построим на нем дерево отрезков. После этого для каждого узла дерева строим еще одно дерево отрезков по координате [math]y[/math], которые находятся на том же отрезке.

К примеру,двумерное дерево размером [math]4 \times 4 :[/math]

Анализ и оценка структуры

Строится такое дерево за линейное время. Структура использует [math]O(n^p)[/math] памяти, и отвечает на запрос за [math]O(log^{p} n)[/math], где [math]p[/math]-размерность дерева.

Ответ на запрос в таком дереве будет производиться так же,как и построение: сначала по координате [math]x_1[/math], затем, когда дошли до какой-либо вершины по первой координате, вызвать запрос от этого же дерева по [math]x_2[/math] и так далее. Получается, что для [math]n-[/math]мерного дерева запрос выполняется за [math]O(log (s_{x_1})\cdot log (s_{x_2})...log (s_{x_n}))[/math] (для рассмотренного двумерного дерева будет [math]log (n) \cdot log (m) [/math] )

Источники

• e-maxx.ru: Дерево отрезков
  
• F. P. Preparata, M.I. Shamos - Вычислительная геометрия Главы о региональном поиске

См. также

• Дерево отрезков. Построение
  
• Сжатое многомерное дерево отрезков
  
• Многомерное дерево Фенвика