Сведение задачи RMQ к задаче LCA
Версия от 18:13, 28 июня 2011; Nikita.Ofitserov (обсуждение | вклад)
Постановка задачи RMQ
Дан массив . Поступают запросы вида , на каждый запрос требуется найти минимум в массиве , начиная с позиции и заканчивая позицией .
Алгоритм
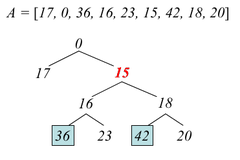
Декартово дерево (англ. сartesian tree) на массиве — это бинарное дерево, рекурсивно определенное следующим образом:
- Корнем дерева является минимальное значение в массиве , скажем .
- Левым поддеревом является декартово дерево на массиве .
- Правым поддеревом является декартово дерево на массиве .
Построим декартово дерево на массиве . Тогда = .
Доказательство
Мы знаем что:
- Любая вершина дерева всегда имеет меньшее значение, чем её дети. Тогда любой предок или меньше их самих.
- ближайший к корню и по п.1 имеет наименьшее значение в своем поддереве. По построению, это поддерево содержит в частности подмассив и находится между и . То есть является
Сложность
Построение дерева наивным алгоритмом . Существует алгоритм построения за .
Препроцессинг для — и ответ на запрос . В итоге получили {построение , запрос }.