Предикат "левый поворот"

Эта статья находится в разработке!

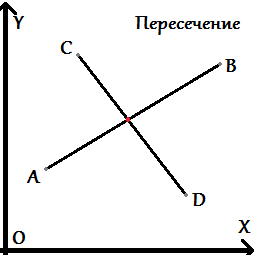
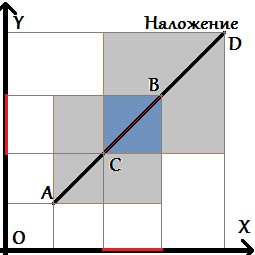
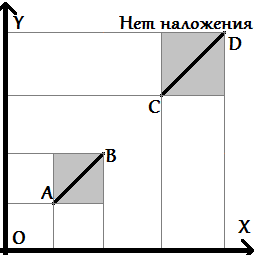
Допустим нам дана задача: Даны два отрезка AB и CD (они могут вырождаться в точки). Требуется проверить, пересекаются они на плоскости или нет. Для упрощения определения этого факта в вычислительной геометрии используется предикат "левый поворот" (или "по часовой стрелке").

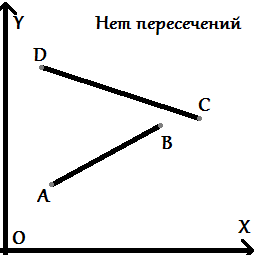
Итак, у нас есть задача, с чего начнем её решать? Какие вообще могут быть расположения точек и самих отрезков относительно друг друга?

Одно из решений - определить, лежат ли точки концов отрезков по разные стороны от другого отрезка. Вот тут нам и поможет наш предикат, где два из трех аргументов (например a и b) это точки концов одного отрезка, а последний - один из концов другого отрезка.

Определение:

Left_Turn(a, b, c) = true, если [math](b - a)[/math]х[math](c - a) \gt 0[/math]

Распишем поподробнее: [math](b - a)[/math] х [math](c - a) = (b_x - a_x)(c_y - a_y) - (b_y - a_y)(c_x - a_x) = A - B[/math]

Какие при этом у нас будут погрешности?

NB: при сложении складываются абс. погрешности,при умножении складываются отн. погрешности.

[math]\delta (b - a)[/math]х[math](c - a) = |A|*\epsilon*((|b_x|+|a_x|)/(|b_x|*|a_x|)+(|c_y|+|a_y|)/(|c_y|*|a_y|)) + [/math]

[math] + |B|*\epsilon*((|b_y|+|a_y|)/(|b_y|*|a_y|)+(|c_x|+|a_x|)/(|c_x|*|a_x|))[/math]

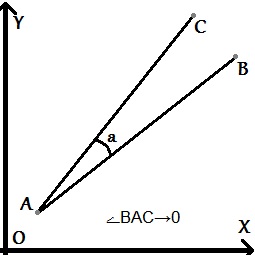
Заметим, что все координаты (а значит и наши вычисления) производятся в вещественных числах, а это значит, что при вычислениях мы можем допустить ошибку. Какую? Посмотрим внимательнее на наш предикат. Ошибка раскрывается тогда, когда угол между отрезками АВ и АС крайне мал.

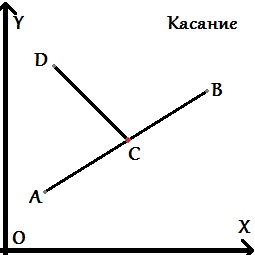
Ещё следует обратить внимание на граничные случаи, когда какие-то точки попадают на саму прямую. При этом возникает единственный особый случай, когда вышеописанные проверки ничего не дадут — случай, когда оба отрезка лежат на одной прямой. Этот случай надо рассмотреть отдельно. Для этого достаточно проверить, что проекции этих двух отрезков на оси X и Y пересекаются (часто эту проверку называют "проверкой на bounding box").