Конфигурация
Версия от 03:54, 2 ноября 2011; Dgerasimov (обсуждение | вклад)
Эта статья находится в разработке!
Общие определения(R^d)
<wikitex>
| Определение: |
| Гиперплоскостью(англ. hyperplane) в $\mathbb{R}^d$ называется его подпространство размерности $\mathbb{R}^{d - 1}$. |
| Определение: |
| Конфигурацией(англ. arrangement) $\mathcal{A}(\mathcal{H})$ называется разбиение $\mathbb{R}^d$ в связные открытые(топологически) ячейки размерностей $0, 1 \dots d $ множеством $\mathcal{H}$ гиперплоскостей в $ \mathbb{R}^d$. |
| Определение: |
| Ячейкой(англ. cell) размерности $d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в $R^d$, не пересекаемая ни одной гиперплоскостью в $\mathcal{H}$. Ячейкой размерности $k$, где $0 \le k < d$ в $\mathcal{A}(\mathcal{H})$ называется максимальная связная область в пересечении гиперплоскостей подмножества $\mathcal{S} \in \mathcal{H}$, которая не пересекается ни одной гиперплоскостью из множества $\mathcal{H} \setminus \mathcal{S}$. //БИДА, сложно обобщить на ограниченные гиперплоскости. |
| Определение: |
| Вершина(англ. vertex) — ячейка размерности 0. Ребро(англ. edge) — ячейка размерности 1. |
Частный случай(R^2)
Замечание: в $\mathbb{R}^2$ ячейками размерности 0 также считаются точки, ограничивающие лучи и отрезки.
Примеры
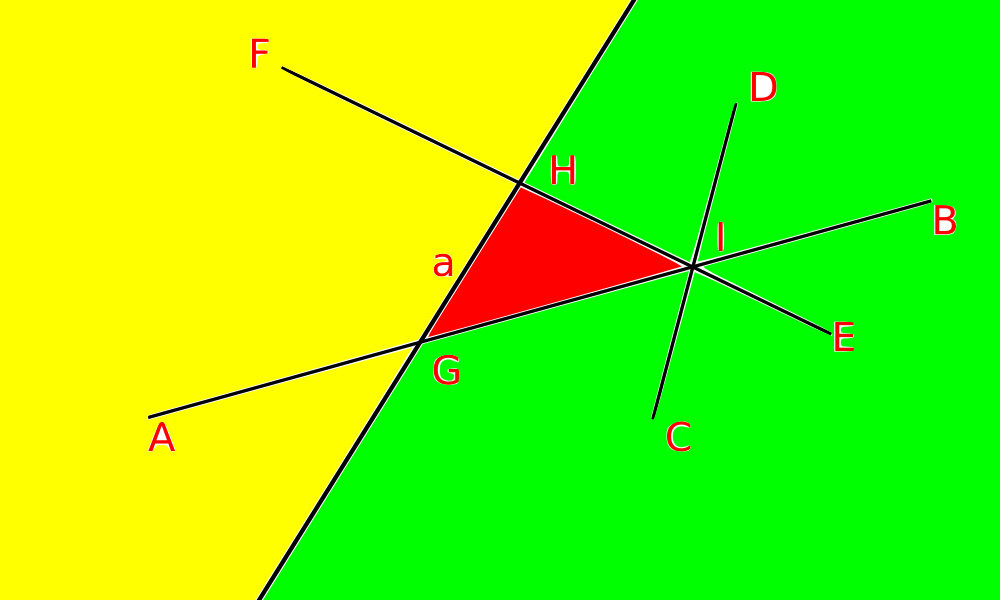
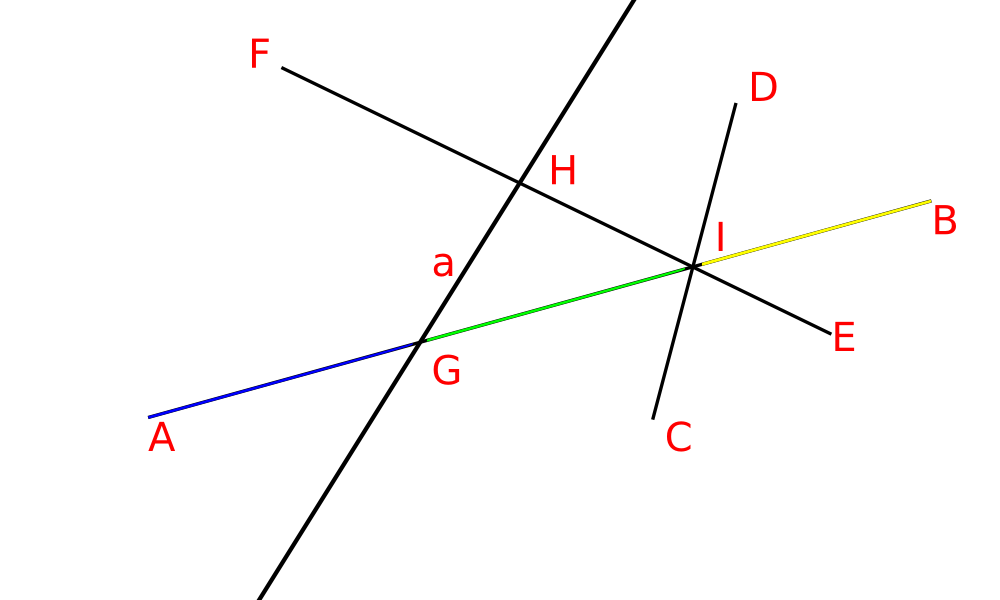
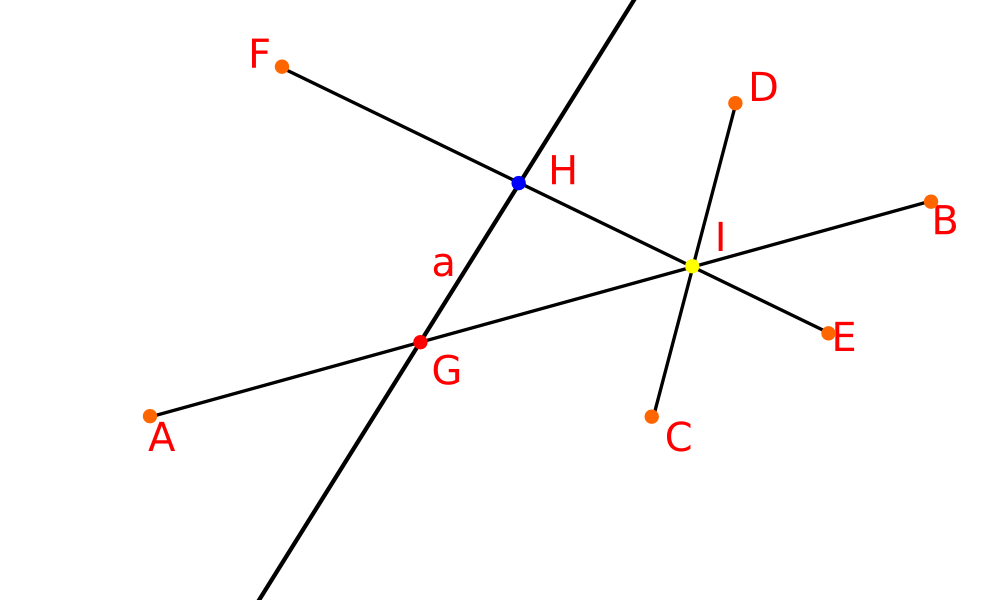
В $\mathbb{R}^2$, гиперплоскостями являются прямые, лучи и отрезки, а конкретно, $\mathcal{H} = \{AB, CD, EF, a\}$
Источники
- Goodman J.E., O'Rourke J. Handbook of discrete and computational geometry. p. 537, 2004, 2nd edition.
</wikitex>