Минимизация ДКА, алгоритм Хопкрофта (сложность O(n log n))

Постановка задачи

Пусть дан автомат, распознающий определенный язык. Требуется найти эквивалентный автомат с наименьшим количеством состояний.

Минимизация ДКА

Понятие эквивалентности состояний позволяет объединить состояния в классы следующим образом.

1. Все состояния в классе эквивалентны.
2. Любые два состояния, выбранные из разных класов, неэквивалентны.

Таким образом, основная идея минимизации ДКА состоит в разбиении множества состояний на классы эквивалентности.

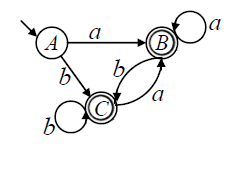
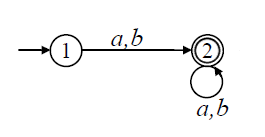
Пример минимизации ДКА

Первый класс состоит из состояния [math]A[/math], а второй из эквивалентных состояний [math]B[/math] и [math]C[/math].

Алгоритм

Алгоритм итеративно строит разбиение множества состояний следующим образом.

1. Первоначальное разбиение множества состояний — класс допускающих состояний и класс недопускающих состояний.
2. Алгоритм помещает оба эти класса в очередь.
3. Из очереди извлекается класс, далее именуемый как сплиттер.
4. Перебираются все символы из алфавита [math]\Sigma[/math], где [math]c[/math] — текущий символ.
5. Все классы текущего разбиения разбиваются на 2 подкласса (один из которых может быть пустым). Первый состоит из состояний, которые по символу [math]c[/math] переходят в сплиттер, а второй из всех оставшихся.
6. Те классы, которые разбились на два непустых подкласса, заменяются этими подклассами в разбиении, а также меньший из двух подклассов добавляется в очередь.
7. Пока очередь не пуста, алгоритм выполняет п.3 – п.6.

Псевдокод

[math]Q[/math] — множество состояний ДКА. [math]F[/math] — множество терминальных состояний. [math]W[/math] — очередь. [math]P[/math] — разбиение множества состояний ДКА. [math]R[/math] — класс состояний ДКА.

 [math]W \leftarrow \{ F, Q \setminus F \}[/math]
 [math]P \leftarrow \{ F, Q \setminus F \}[/math]
 while not [math]W[/math].isEmpty() 
   [math]W[/math].pop([math]S[/math])
   for all [math]a \in \Sigma[/math]
     for all [math]R[/math] in [math]P[/math] 
       [math]R_1 = R \cap \delta^{-1} (S, a) [/math]
       [math]R_2 = R \setminus R_1[/math]
       if [math] |R_1| \ne 0[/math] and [math]|R_2| \ne 0[/math]
         replace [math]R[/math] in [math]P[/math] with [math]R_1[/math] and [math]R_2[/math]
           if [math] |R_1| \le |R_2|[/math]
             [math]W[/math].push([math]R_1[/math])
           else
             [math]W[/math].push([math]R_2[/math])

Время работы алгоритма

Благодаря системе добавления классов состояний в очередь, каждое ребро будет рассмотрено не более чем [math]\log{n}[/math] раз. А так как ребер у нас порядка [math] |\Sigma| * n [/math] то получаем [math] O(n\log{n})[/math]

Литература

• Хопкрофт Д., Мотвани Р., Ульман Д. Введение в теорию автоматов, языков и вычислений, 2-е изд. : Пер. с англ. — М.: Издательский дом «Вильямс», 2002. — С. 177 — ISBN 5-8459-0261-4 (рус.)
• J. E. Hopcroft. An n log n algorithm for minimizing states in a finite automaton. Technical Report CS-71-190, Stanford University, January 1971.