Граф блоков-точек сочленения

Определение:

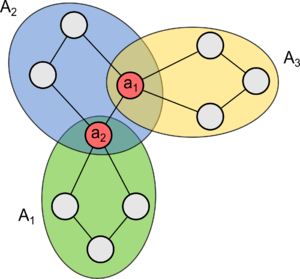
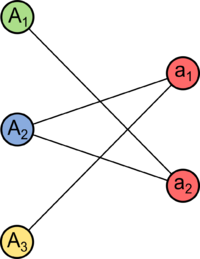
Пусть граф [math]G[/math] связен. Обозначим [math]A_1...A_n[/math] — блоки, а [math]a_1...a_m[/math] — точки сочленения [math]G[/math]. Построим двудольный граф [math]T[/math], поместив [math]A_1...A_n[/math] и [math]a_1...a_m[/math] в различные его доли. Если точка сочленения принадлежит блоку, проведем между ними ребро. Полученный граф [math]T[/math] называют графом блоков-точек сочленения графа [math]G[/math].

Граф [math]G[/math]

Граф [math]T[/math]

Лемма:

В определении, приведенном выше, [math]T[/math] — дерево.

Доказательство:

[math]\triangleright[/math]

Достаточно показать, что в [math]T[/math] нет циклов. Пусть [math]A_i, a_k, A_j: a_k \in A_i, A_j[/math] — последовательные вершины [math]T[/math], лежащие на цикле. Тогда существует последовательность точек сочленения и блоков, соединяющая [math]A_i[/math] и [math]A_j[/math] и не содержащая [math]a_k[/math]. По ней можно проложить путь в [math]G[/math] (можем переходить из блока в блок по точке сочленения и из одной части блока в другую) и замкнуть его в вершине [math]a_k[/math], получив цикл, что противоречит тому, что [math]a_k[/math] — точка сочленения.

[math]\triangleleft[/math]

Литература

М.О.Асанов, В.А.Баранский, В.В.Расин ДИСКРЕТНАЯ МАТЕМАТИКА: ГРАФЫ, МАТРОИДЫ, АЛГОРИТМЫ

См. также

• Граф компонент реберной двусвязности