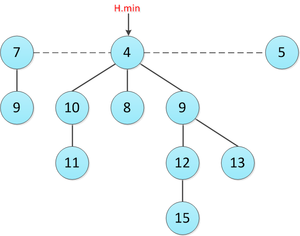
Фибоначчиева куча

Фибоначчиево дерево

Определение:

Фибоначчиево дерево — биномиальное дерево, где у каждой вершины удалено не более одного ребенка.

Определение:

Порядок фибоначчиева дерева — порядок соответствующего биномиального дерева, из которого оно получено.

Лемма:

Для всех целых [math] n \geqslant 2[/math] [math] F_n = 1 + \sum\limits_{i=0}^{n-2} F_i [/math], где [math] F_n [/math] — [math] n [/math]-ое число Фибоначчи, определяемое формулой: [math] F_n = \begin{cases} 0, & n = 0 \\ 1, & n = 1 \\ F_{n-1} + F_{n-2}, & n \geqslant 2 \end{cases} [/math]

Доказательство:

[math]\triangleright[/math]

Докажем лемму по индукции: при [math]n = 2[/math] [math]F_2 = 1 + \sum\limits_{i=0}^0 F_i = 1 + 0 = 1[/math], что действительно верно. По индукции предполагаем, что [math]F_{n-1} = 1 + \sum\limits_{i=0}^{n-3} F_i [/math]. Тогда [math]F_n = F_{n-1} + F_{n-2} = 1 + \sum\limits_{i=0}^{n-3} F_i + F_{n-2} = 1 + \sum\limits_{i=0}^{n-2} F_i[/math]

[math]\triangleleft[/math]

Лемма:

Фибоначчиево дерево порядка [math]n[/math] содержит не менее [math]F_n[/math] вершин.

Доказательство:

[math]\triangleright[/math]

Докажем это утверждение по индукции. Пусть [math]s_n[/math] — минимальный размер фибоначчиева дерева порядка n. При [math]n = 0[/math] [math]s_0 = 1 \gt F_0[/math]. При [math]n = 1[/math] [math]s_1 = 1 = F_1[/math]. Предположим по индукции, что для всех [math]i \lt n \ s_i \geqslant F_i[/math]. Пусть в нашем дереве удалено поддерево порядка [math]n - 1[/math]. Тогда [math]s_n = 1 + \sum\limits_{i=0}^{n-2} s_i \geqslant 1 + \sum\limits_{i=0}^{n-2} F_i[/math] Но по предыдущей лемме [math]1 + \sum\limits_{i=0}^{n-2} F_i = F_n[/math]. Следовательно, [math]s_n \geqslant F_n[/math]

[math]\triangleleft[/math]

Фибоначчиева куча

Определение:

Фибоначчиева куча — набор фибоначчиевых деревьев, упорядоченных в соответствии со свойством неубывающей кучи.

Фибоначчиевы кучи поддерживают тот же набор операций, что и биномиальные кучи, но имеют то преимущество, что операции, в которых не требуется удаление, имеют амортизированное время работы, равное [math]O(1)[/math].

С теоретической точки зрения фибоначчиевы кучи особенно полезны в случае, когда количество операций [math]extractMin[/math] и [math]delete[/math] относительно мало по сравнению с количеством других операций. Однако с практической точки зрения программная сложность и высокие значения постоянных множителей в формулах времени работы существенно снижают эффективность применения фибоначчиевых куч, делая их в большинстве случаев менее привлекательными, чем обычные бинарные кучи.

Определение:

Степень вершины — порядок фибоначчиева дерева, чьим корнем эта вершина является.

Лемма:

[math]F_n =\Theta(\varphi^n)[/math], где [math] \varphi = \frac {1 + \sqrt 5} {2}[/math]

Доказательство:

[math]\triangleright[/math]

Для начала докажем, что [math]F_n =[/math] [math]\frac {\varphi^n - (-\varphi)^{-n}} {\sqrt 5}[/math] Используем для этого математическую индукцию. При [math]n = 0[/math] [math]F_0 =[/math] [math]\frac {\varphi^0 - (-\varphi)^0} {\sqrt 5} = \frac {1 - 1} {\sqrt 5} = 0[/math], что верно. При [math]k = 1[/math] [math]F_1 =[/math] [math]\frac {\varphi^1 - (-\varphi)^{-1}} {\sqrt 5} = \frac {1} {\sqrt 5}(\frac {1 + \sqrt 5} {2} - \frac {1 - \sqrt 5} {2}) = \frac {2\sqrt 5} {2\sqrt 5} = 1[/math], что также верно. По индукции предполагаем, что [math]F_{n-1} =[/math] [math]\frac {\varphi^{n-1} - (-\varphi)^{1-n}} {\sqrt 5}[/math] и [math]F_{n-2} =[/math] [math]\frac {\varphi^{n-2} - (-\varphi)^{2-n}} {\sqrt 5}[/math]. Тогда [math]F_n = F_{n-1} + F_{n-2} =[/math] [math]\frac {\varphi^{n-1} - (-\varphi)^{1-n}} {\sqrt 5} + \frac {\varphi^{n-2} - (-\varphi)^{2-n}} {\sqrt 5} =[/math] [math]= \frac {1} {\sqrt 5}[/math] [math](\varphi^{n-1} - (-\varphi)^{1-n} + \varphi^{n-2} - (-\varphi)^{2-n}) [/math] [math]= \frac {1} {\sqrt 5}[/math] [math](\varphi^{n}(\varphi^{-1} + \varphi^{-2}) - (-\varphi)^{-n}(-\varphi + \varphi^{2}))[/math] Подставив вместо [math]\varphi[/math] его значение, нетрудно убедится, что [math]\varphi^{-1} + \varphi^{-2} = -\varphi + \varphi^{2} = 1[/math] Поскольку [math]\left\vert (-\varphi)^{-1} \right\vert \lt 1[/math], то выполняются неравенства [math]\frac {(-\varphi)^{-n}} {\sqrt 5} \lt \frac {1} {\sqrt 5} \lt \frac {1} {2}[/math]. Таким образом, [math]n[/math]-е число Фибоначчи равно [math]\frac {\varphi^{n}} {\sqrt 5}[/math], округленному до ближайшего целого числа. Следовательно, [math]F_n =\Theta(\varphi^n)[/math].

[math]\triangleleft[/math]

Лемма:

Максимальная степень [math]D(n)[/math] произвольной вершины в фибоначчиевой куче с [math]n[/math] вершинами равна [math]O(\log(n))[/math]

Доказательство:

[math]\triangleright[/math]

Пусть [math]x[/math] — произвольная вершина в фибоначчиевой куче с [math]n[/math] вершинами, и пусть [math]k[/math] — степень вершины [math]x[/math]. Тогда по доказанному выше в дереве, корень которого [math]x[/math], содержится не менее [math]F_k[/math] вершин, что в свою очередь по лемме равно [math]\Theta(\varphi^k)[/math]. То есть [math]n \geqslant \varphi^{k}[/math] Логарифмируя по основанию [math]\varphi[/math], получаем [math]\log_{\varphi}n \geqslant k[/math] Таким образом, максимальная степень [math]D(n)[/math] произвольной вершины равна [math]O(\log(n))[/math].

[math]\triangleleft[/math]

Структура

Пример фибоначчиевой кучи

• Каждый узел [math]x[/math] в куче [math]H[/math] содержит следующие указатели и поля:
  • [math]x.key[/math] — поле, в котором хранится ключ;
  • [math]x.p[/math] — указатель на родительский узел;
  • [math]x.child[/math] — указатель на один из дочерних узлов;
  • [math]x.left[/math] — указатель на левый сестринский узел;
  • [math]x.right[/math] — указатель на правый сестринский узел;
  • [math]x.degree[/math] — поле, в котором хранится количество дочерних узлов;
  • [math]x.mark[/math] — логическое значение, которое указывает, были ли потери узлом [math]x[/math] дочерних узлов, начиная с момента, когда [math]x[/math] стал дочерним узлом какого-то другого узла.
• Дочерние узлы [math]x[/math] объединены при помощи указателей [math]left[/math] и [math]right[/math] в циклический двусвязный список.
• Корни всех деревьев в [math]H[/math] связаны при помощи указателей [math]left[/math] и [math]right[/math] в циклический двусвязный список корней.
• Обращение к [math]H[/math] выполняется посредством указателя [math]H.min[/math] на корень дерева с минимальным ключом. Этот узел называется минимальным узлом [math]H[/math].
• Текущее количество узлов в [math]H[/math] хранится в [math]H.size[/math].

Циклический двусвязный список обладает двумя преимуществами для использования в фибоначчиевых кучах. Во-первых, удаление элемента из такого списка выполняется за время [math]O(1)[/math]. Во-вторых, если имеется два таких списка, их легко объединить в один за то время [math]O(1)[/math].

Потенциал

Для анализа производительности операций введем потенциал для фибоначчиевой кучи [math]H[/math] как [math] \Phi(H) = t[H] + 2m[H] [/math], где [math] t[H] [/math] — количество элементов в корневом списке кучи, а [math] m[H] [/math] — количество вершин, у которых удален один ребенок (то есть вершин с пометкой [math] x.mark = true [/math]). Договоримся, что единицы потенциала достаточно для оплаты константного количества работы. На языке метода предоплаты это выглядит следующим образом: возле каждого корня лежит одна монета, а возле каждой вершины, у которой удалили ребенка, лежит две монеты.

Операции

Рассмотрим операции, которые поддерживают фибоначчиевы кучи. Амортизированное время их работы показано в таблице.

[math]makeHeap[/math]	[math]O(1)[/math]
[math]insert[/math]	[math]O(1)[/math]
[math]getMin[/math]	[math]O(1)[/math]
[math]merge[/math]	[math]O(1)[/math]
[math]extractMin[/math]	[math]O(\log(n))[/math]
[math]decreaseKey[/math]	[math]O(1)[/math]
[math]delete[/math]	[math]O(\log(n))[/math]

Стоит заметить, что структура фибоначчиевых куч, также как биномиальных и бинарных, не могут обеспечить эффективную реализацию поиска элемента с заданным ключом, поэтому операции [math]decreaseKey[/math] и [math]delete[/math] получают в качестве аргумента указатель на узел, а не значение его ключа.

makeHeap

Создается новый пустой корневой список, в [math] H.min [/math] устанавливается значение [math] null [/math]. Реальное время работы — [math] O(1) [/math].

insert

Вставка элемента в фибоначчиеву кучу также тривиальна: создается новая куча из одного элемента и сливается с текущей. Амортизированная стоимость операции: 1 (создание кучи) + 2 (слияние куч + релаксация минимума) + 1(изменение потенциала) = 4 = [math] O(1) [/math].

getMin

Возвращает указатель [math]H.min[/math]. Реальное время работы — [math] O(1) [/math]

merge

Слияние двух фибоначчиевых куч происходит просто: объединяем списки этих куч в один, релаксируем минимум. Реальное время работы — [math] O(1) [/math]. Амортизированное время работы также [math] O(1) [/math], поскольку, при объединении двух куч в одну, потенциалы обеих куч суммируются, итоговая сумма потенциалов не изменяется, [math] \Phi_{n + 1} - \Phi_n = 0 [/math].

extractMin

Первая рассматриваемая операция, в ходе которой меняется структура кучи. Здесь используется вспомогательная процедура [math] consolidate [/math]. Возьмем указатель на [math] H.min [/math], удалим эту вершину. Ее поддеревья (их не более, чем [math] D(n) [/math], где [math] D(n) [/math] — максимальная степень вершины в куче) объединим с корневым списком. Теперь вызываем процедуру [math] consolidate [/math]. После этой операции в списке корней остается не более чем [math] D(n) + 1[/math] узлов, среди которых нужно найти минимальный. Итоговая асимптотика операции [math]extraxtMin[/math], учитывая и вспомогательную функцию [math] consolidate [/math], время работы которой доказывается ниже, равно: [math] O(1)+O(D(n))+O(D(n))=O(D(n)) [/math]. Но по доказанной выше лемме это [math]O(\log(n))[/math].

consolidate

Данная процедура принимает кучу и преобразует ее таким образом, что в корневом списке остается не более [math] D(n) + 1[/math] вершин.

Для этого возьмем массив списков указателей на корни деревьев [math] A[0..D[H]] [/math], где [math] D[H] [/math] — максимальная степень вершины в текущем корневом списке.

Затем происходит процесс, аналогичный слиянию биномиальных куч: добавляем поочередно каждый корень, смотря на его степень. Пусть она равна [math] d [/math]. Если в соответствующей ячейке [math]A[/math] еще нету вершины, записываем текущую вершину туда. Иначе подвешиваем одно дерево к другому, и пытаемся также добавить дерево, степень корня которого уже равна [math] d + 1 [/math]. Продолжаем, пока не найдем свободную ячейку.

Учетная стоимость [math] consolidate [/math] равна [math] O(D(n)) [/math]. Докажем это:

Изначально в корневом списке было не более [math] D(n) + t[H] - 1 [/math] вершин, поскольку он состоит из исходного списка корней с [math]t[H][/math] узлами, минус извлеченный узел и плюс дочерние узлы, количество которых не превышает [math] D(n) [/math]. В ходе операции [math] consolidate [/math] мы сделали [math] O(D(n) + t[H]) [/math] слияний деревьев. Потенциал перед извлечением минимума равен [math] t[H] + 2m[H] [/math], а после не превышает [math] D(n) + 1 + 2m[H] [/math], поскольку в корневом списке остается не более [math] D(n) + 1 [/math] узлов, а количество помеченных узлов не изменяется. Таким образом, амортизированная стоимость не превосходит

[math] O(D(n) + t[H]) + (D(n) + 1 + 2m[H]) - (t[H] + 2m[H]) = O(D(n)) + O(t[H]) - t[H][/math]

Поскольку мы договорились, что можем масштабировать единицу потенциала таким образом, чтобы покрывать константное количество работы, то итоговая амортизационная оценка — [math] O(D(n)) [/math]

decreaseKey

Основная идея: хотим, чтобы учетная стоимость данной операции была [math] O(1) [/math]. Было бы хорошо, чтобы вершина не всплывала до корня, и тогда дерево не придется сильно перестраивать. Для этого при удобном случае будем вырезать поддерево полностью и перемещать его в корневой список. Итак, сам алгоритм:

1. Проверяем, если новое значение ключа все же не меньше значения ключа родителя, то все хорошо, и мы выходим.
2. Иначе, вырезаем дерево с текущей вершиной в корневой список, и производим каскадное вырезание родителя.

cut

При вырезании вершины мы удаляем ее из списка детей своего родителя, уменьшаем степень ее родителя ([math] x.p.degree [/math]) и снимаем пометку с текущей вершины ([math] x.mark = false [/math]).

cascadingCut

Пример каскадного вырезания

Перед вызовом каскадного вырезания нам известно, удаляли ли ребенка у этой вершины. Если у вершины до этого не удаляли дочерний узел ([math] x.mark = false [/math]), то мы помечаем эту вершину ([math] x.mark = true [/math]) и прекращаем выполнение операции. В противном случае применяем операцию [math]cut[/math] для текущей вершины и запускаем каскадное вырезание от родителя.

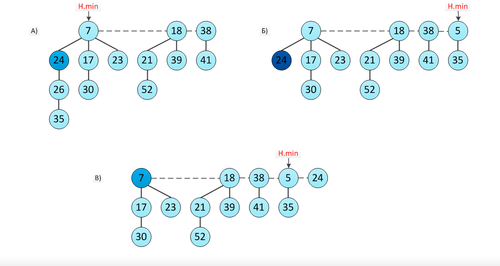
Пример

Рисунок иллюстрирует пример каскадного вырезания:

• Изначально, куча состояла из 3 фибоначчиевых деревьев. У вершины с ключом 24 отсутствует 1 ребенок.
• Уменьшаем ключ 26 до 5 и делаем операцию [math]cut[/math] этого дерева. Получаем кучу с 4 деревьями и новым минимумом. Но у вершины с ключом 24 был удален второй ребенок, поэтому запускам операцию [math]cascadingCut[/math] для этой вершины: вырезаем ее, помещаем в корневой список и помечаем ее родителя.
• У вершины с ключом 7 удален лишь один ребенок, поэтому операция [math]cascadingCut[/math] от нее не запускается. В итоге, получаем кучу, состоящую из 5 фибоначчиевых деревьев.

Время работы

Докажем, что амортизированное время работы операции [math]decreaseKey[/math] есть [math] O(1) [/math]. Поскольку в процедуре нет циклов, ее время работы определяется лишь количеством рекурсивных вызовов каскадного вырезания.

Пусть мы вызвали процедуру каскадного вырезания [math] k [/math] раз. Тогда вершин с пометкой [math] x.mark = true [/math] стало на [math] k [/math] меньше, а в корневом списке прибавилось [math] k [/math] новых вершин. Итого, время работы будет: [math] O(k) + \Phi_i - \Phi_{i - 1} = O(k) + (k - 2k + O(1)) [/math]. Следовательно, амортизированная стоимость не превышает [math] O(1) [/math], поскольку мы можем соответствующим образом масштабировать единицы потенциала.

На языке метода предоплаты: пусть у каждого узла в списке корней лежит монета, а у каждой помеченной вершины — 2 монеты. Покажем, что взяв 4 монеты за операцию [math] decreaseKey [/math], мы сможем оплатить эту операцию. Одну монету потратим на перенос в корневой список и релаксацию минимума, еще 1 — на то, чтобы положить монету у новой вершины в корневом списке, которую мы потратим на следующую операцию [math]extractMin[/math]. У нас осталось 2 монеты. Далее производим каскадное вырезание: в случае, когда [math] x.p.mark = false [/math], кладем 2 монеты к этой вершине, и устанавливаем соответствующую пометку. Инвариант сохраняется.

Иначе, добавляем к помеченной вершине родителя еще 2 монеты. В итоге, в родительском узле становится 4 монеты, и мы можем рекурсивно продолжить данный процесс. Оценка доказана.

delete

Удаление вершины реализуется через уменьшение ее ключа до [math] -\infty [/math] и последующим извлечением минимума. Амортизированное время работы: [math] O(1) + O(D(n)) = O(D(n)) [/math].

Поскольку ранее мы показали, что [math] D(n) = O(\log(n)) [/math], то соответствующие оценки доказаны.

Источники

• Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн — Алгоритмы: построение и анализ. — М.: Издательский дом «Вильямс», 2005. — С. 1296. — ISBN 5-8459-0857-4
• Числа Фибоначчи — Википедия
• Фибоначчиева куча — Википедия
• Фибоначчиевы кучи — INTUIT.ru
• Визуализаторы
• Fibonacci Heaps