Сортировка слиянием
Содержание
Сортировка слиянием
Сортировка слиянием — очень простой алгоритм сортировки. Он был предложен Джоном фон Нейманом в 1945 году.
Это стабильный алгоритм сортировки, использующий дополнительной памяти и времени.
Принцип работы
Данный алгоритм — хороший пример использования принципа «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи.
Процедура слияния требует два отсортированных массива. Заметив, что массив из одного элемента по определению является отсортированным, мы можем осуществить сортировку следующим образом:
1. Разбить имеющиеся элементы массива на пары и осуществить слияние элементов каждой пары, получив отсортированные цепочки длины 2 (кроме, быть может, одного элемента, для которого не нашлось пары).
2. Разбить имеющиеся отсортированные цепочки на пары, и осуществить слияние цепочек каждой пары.
3. Если число отсортированных цепочек больше единицы, перейти к шагу 2.
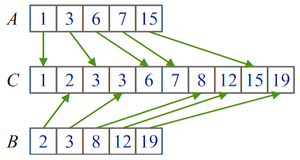
Слияние 2-х массивов
Допустим, у нас есть два отсортированных массива А и B размерами и соответственно, и мы хотим объединить их элементы в один большой отсортированный массив C размером . Для этого можно применить процедуру слияния, суть которой заключается в повторяющемся «отделении» элемента, наименьшего из двух имеющихся в началах исходных массивов, и присоединении этого элемента к концу результирующего массива. Элементы мы переносим до тех пор, пока один из исходных массивов не закончится. После этого оставшийся «хвост» одного из входных массивов дописывается в конец результирующего массива. Пример работы процедуры показан на рисунке:
Алгоритм слияния формально можно записать следующим образом:
// слияние двух массивов с помощью временного merge (array a, array b) // a - левая половина (от l до m), b - правая половина (от m + 1 до r) i = l, j = m + 1, k = 0; array temp; while i <= m and j <= r temp[k++] = (a[j] < b[i]) ? a[j++] : b[i++]; while i <= m temp[k++] = b[i++]; while j <= r temp[k++] = a[j++]; for (int t = 0; t != k; t++) a[t] = temp[t] // в конце a[1..k] это будет отсортированный массив
Рекурсивный алгоритм
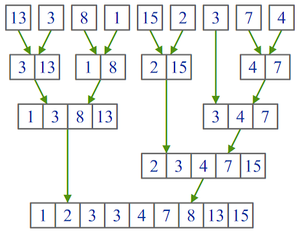
Проще всего формализовать этот алгоритм рекурсивным способом. Функция сортирует участок массива от элемента с номером a до элемента с номером b:
// r и l - правая и левая граница массива, m - середина m = r / 2 // делим на 2 половины if m == r // условие выхода - если массив стал состоять из 1 элемента return sort a[l..m] // рекурсивная сортировка правой и левой частей, в функцию передаются левая и правая границы массива sort a[m+1..r] merge (a[l..m], a[m+1..r]) // делаем процедуру слияния 2х отсортированных половинок
Пример работы алгоритма показан на рисунке:
Время работы
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай - время сортировки массива длины n, тогда для сортировки слиянием справедливо
( - это время, необходимое на то, чтобы слить два массива). Распишем это соотношение:
Осталось оценить . Мы знаем, что , а значит . Уравнение примет вид . Так как - константа, то .
Свойства
Стабильный.
дополнительной памяти для массива.
дополнительной памяти для связных списков.
времени.