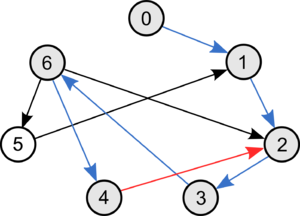
Использование обхода в глубину для поиска цикла
Содержание
Постановка задачи
Пусть дан ориентированный граф без петель и кратных рёбер. Требуется проверить наличие цикла в этом графе.
Решим эту задачу с помощью поиска в глубину за .
Алгоритм
Произведём серию поисков в глубину в графе. Т.е. из каждой вершины, в которую мы ещё ни разу не приходили, запустим поиск в глубину, который при входе в вершину будет красить её в серый цвет, а при выходе - в чёрный. И если поиск в глубину пытается пойти в серую вершину, то это означает, что мы нашли цикл.
Сам цикл можно восстановить проходом по массиву предков.
Доказательство
Пусть дан граф . Запустим . Рассмотрим выполнение процедуры поиска в глубину от некоторой вершины . Так как все серые вершины лежат в стеке рекурсии, то для них вершина достижима, так как между соседними вершинами в стеке есть ребро. Тогда если из рассматриваемой вершины существует ребро в серую вершину , то это значит, что из вершины существует путь в и из вершины существует путь в состоящий из одного ребра. И так как оба эти пути не пересекаются, то цикл существует.
Докажем, что если в графе существует цикл, то его всегда найдет. Пусть - первая вершина принадлежащая циклу, рассмотренная поиском в глубину. Тогда существует вершина , принадлежащая циклу и имеющая ребро в вершину . Так как из вершины в вершину существует белый путь (они лежат на одном цикле), то по лемме о белых путях во время выполнения процедуры поиска в глубину от вершины , вершина будет серой. Так как из есть ребро в , то это ребро в серую вершину. Следовательно нашел цикл.
Реализация
Здесь приведена реализация алгоритма.
Псевдокод
int graph[][];
int color[];
dfs(int index)
color[index] = grey; // красит вершину в серый цвет
for (v : uv - ребро)
if ( color[v] == white )
dfs(v);
if ( color[v] == grey )
print(); // вывод ответа
color[index] = black; // красит вершину в черный цвет
Литература
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ.[1] — 2-е изд. — М.: Издательский дом «Вильямс», 2007. — С. 1296.