Многомерное дерево отрезков

Материал из Викиконспекты
Перейти к: навигация, поиск

Дерево отрезков естественным образом обобщается на двумерный и вообще говоря многомерный случай. Такая структура данных может вычислять значение некоторой ассоциативной функции на гиперпрямоугольнике. Например, она позволяет решать следующую задачу. Дан [math]p[/math]-мерный массив, где индекс каждого измерения массива может принимать значения от 1 до [math]n[/math]. Необходимо уметь изменять значение элемента массива, а также находить сумму на [math]p[/math]-мерной области. Каждую из этих операций многомерное дерево отрезков выполняет за [math]O(\log^{p} n)[/math].

Принцип работы

Пример некоторой стадии работы алгоритма (поиск элементов, подходящих некоторой области)

[math]n[/math]-мерное дерево отрезков — обычное дерево отрезков, элементами которого являются деревья отрезков размерности на 1 меньше. Основная идея заключается в рекурсивном переходе к деревьям меньшей размерности. Рассмотрим работу этого принципа на следующем примере. Пусть задано [math]p[/math]-мерное пространство с координатными осями [math]x_1, x_2, x_3...x_p[/math]. Необходимо найти значение некоторой ассоциативной функции на гиперпрямоугольнике.

Функция, вычисляющая ответ, должна работать следующим образом. На вход она принимает [math]i[/math]-мерное дерево отрезков, которое соответствует рассматриваемой области (где [math]i[/math] — количество координатных осей, которые не были рассмотрены), а также [math]i[/math]-мерную область, для которой следует вычислить функцию. Вначале она находит [math]i-1[/math]-мерные деревья отрезков, которые соответствуют отрезку по [math]p-i+1[/math] координате, и рекурсивно запускается от них (если текущее дерево одномерное, то функция просто возвращает ответ из соответствующего листа). После этого считает итоговый результат, используя полученные после рекурсивных вызовов значения.

Для того, чтобы определить, от каких именно деревьев отрезков следует запускаться рекурсивно, действовать необходимо так же, как и в одномерном случае. Т. е. если текущий отрезок не пересекается с необходимым, то возвращаем нейтральный элемент, если он полностью лежит в необходимом отрезке, то рекурсивно переходим к следующей размерности, иначе разобьем текущий отрезок пополам, и рассмотри отдельно каждую из частей.

На рисунке справа показан пример обработки очередной координаты (поиск соответствующих отрезку элементов — деревьев на 1 меньшей мерности).

Таким образом, алгоритм совершит [math]p[/math] вхождений в рекурсию, каждая итерация которой работает за [math]O(\log n)[/math] и получим необходимую асимптотику.

Хранение

Пример двумерного дерева отрезков для 16 элементов

Пусть необходимо хранить дерево отрезков для [math]p[/math]-мерной области, размеры которой [math]n_1 \times n_2 \times ... \times n_p[/math]. Удобнее всего это делать с помощью [math]p[/math]-мерного массива. Однако его размеры по каждой координате, так же как и в одномерном случае, должны превышать размеры соответствующего отрезка в 4 раза. Т. е. потребуется массив размером [math]4 n_1 \times 4 n_2 \times ... \times 4 n_p[/math]. Так двумерное дерево отрезков удобно хранить в виде массива, размером [math]4N \times 4M[/math]. Каждая строчка такого массива соответствует некоторому отрезку по первой координате. Сама же строчка является деревом отрезков по второй координате.

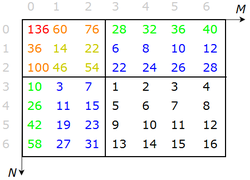
На рисунке справа показан пример дерева отрезков для суммы на массиве 4 на 4, заполненного числами от 1 от 16. Например, в элементе [math]a[2][0] = 100[/math] хранится сумма элементов, соответствующих отрезку [math][2..3][/math] по первой координате и [math][0..3][/math] по второй в исходном массиве. А в ячейке [math]a[0][0] = 136[/math] хранится сумма всех элементов.

Интересно, что если построить дерево вначале по второй координате, а потом по первой, то получившийся массив будет таким же. Т. е. данный двумерный массив можно рассматривать как массив деревьев отрезков, где каждое дерево соответствует некоторому отрезку по второй координате, а в нем хранятся суммы по первой.

Заметим, что в общем случае для хранения [math]p[/math]-мерного дерева отрезков требуется [math]4^p n[/math] памяти, где [math]n[/math] — общее количество элементов.

Многомерный случай

Рассмотрим, как изменяться функции при переходе к [math]n[/math]-мерному случаю.

Например, для операции обновления дерева отрезков изменения будут следующими. В коде будут присутствовать [math]n[/math] функций update (для каждой из координат). Реально будут только две различные реализации этих функций (первая, при нахождении необходимых листьев дерева, рекурсивно переходит к следующей координате, вторая — только возвращает значение из массива). Мы можем не писать [math]n[/math] одинаковых реализаций в коде, но тогда дерево отрезков придется хранить не в [math]n[/math]-мерном массиве, а в одномерном (это не сильно усложнит реализацию, но понятность кода уменьшится).

Рассмотрим более подробно устройство такой функции. В качестве параметров она должна принимать область, на которой считается операция, информацию о том, из каких ячеек массива мы рекурсивно спустились, отрезок, который обрабатывается по текущей координате и необходимый нам отрезок, а также номер текущей ячейки массива. 

operationCalc(area[], x1, x2, ..., xP, leftBorder, rightBorder, needLeft, needRight, vertex)

Вначале следует проверить, что обрабатываемый отрезок не пустой (иначе вернуть нейтральный элемент для операции) 

if needLeft > needRight
 return 0

Потом, если текущий отрезок совпадает с искомым, необходимо перейти к поиску по следующей координате 

if leftBorder == needLeft && rightBorder == needRight
 return operationCalc(area[], x1, x2, ..., xP, vertex, 0, m - 1, area[P + 2].left, area[P + 2].right, 0)

Если же отрезок не совпадает, то делим его пополам и рекурсивно вызываемся от его частей 

med = (leftBorder + rightBorder) / 2
return operationCalc(area[], x1, x2, ..., xP, leftBorder, med, needLeft, min(needRight, med), vertex * 2 + 1) [math]\times[/math]
       operationCalc(area[], x1, x2, ..., xP, med + 1, rightBorder, max(needLeft, med + 1), needRight, vertex * 2 + 2)

В реализации для последней координаты вместо рекурсивного перехода следует вернуть значение из массива 

if leftBorder == needLeft && rightBorder == needRight
 return t[x1][x2]...[xP][vertex]

Теперь рассмотрим операцию обновления. По аналогии напишем [math]n[/math] функций, в каждой из которых сделаем следующее:

  • Если рассматриваемый отрезок содержит больше одного элемента, разобьем его на две части и рекурсивно перейдем в ту, где находится необходимый элемент
  • Перейдем к следующей координате или обновим массив (для последней координаты)

Псевдокод: 

update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, rightBorder, vertex)
 if leftBorder == rightBorder
  if последняя координата
   for I = 1..n
    if xILeft != xIRigth
     t[x1][x2]...[xP][vertex] = t[x1][x2]...[xI * 2 + 1]...[vertex] [math]\times[/math] t[x1][x2]...[xI * 2 + 2]...[vertex]
     return
   t[x1][x2]...[xP][vertex] = newElem.value
  else
   update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)
 else
  med = (leftBorder + rightBorder) / 2
  if med >= newElem.x(P+1)
   update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, leftBorder, med, vertex * 2 + 1)
  else
   update(newElem, x1, x2, ..., xP, x1Left, x1Right, x2Left, x2Right, ..., xPLeft, xPRight, med + 1, vertex * 2 + 2)
  update(newElem, x1, x2, ..., xP, vertex, x1Left, x1Rigth, x2Left, x2Right, ..., leftBorder, rightBorder, 0, m - 1, 0)

Источники

См. также

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Многомерное_дерево_отрезков&oldid=23262»