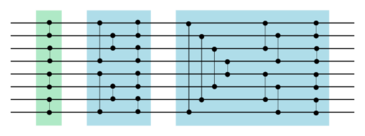
Сеть Бетчера

Эта статья находится в разработке!

Сеть Бетчера (Batcher odd-even mergesort) — сортирующая сеть размером [math]O(n \log^2n)[/math] и глубиной [math]O(\log^2n)[/math], где [math]n[/math] — количество элементов для сортировки.

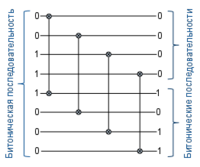
Битоническая последовательность

Сначала введем все необходимые понятия для построения сортирующей сети Бетчера.

Определение:

Битонической последовательностью называется последовательность, которая сначала монотонно возрастает, а затем монотонно убывает, или последовательность, которая приводится к такому виду путем циклического сдвига.

Здесь мы будем рассматривать только нуль-единичные битонические последовательности:

Определение:

Нуль-единичные битонические последовательности — последовательности вида [math]0^i1^j0^k[/math] или [math]1^i0^j1^k[/math] для целых [math]i,j,k\ge0[/math], где [math]1^i[/math] или [math]0^i[/math] обозначает [math]i[/math] идущих подряд единиц или нулей соответственно.

В качестве примеров нуль-единичной битонической последовательности можно привести последовательности [math]00111000[/math], [math]11000111[/math], [math]1110[/math], [math]1[/math], [math]000[/math].
С первого взгляда битонические последовательности могут показаться бесполезными в деле построения сортирующих сетей, но на самом деле они обладают одним полезным свойством: если соединить вместе две отсортированные последовательности, причем одна из них должна быть отсортировала по возрастанию, а другая по убыванию — то получится битоническая последовательность. Далее этому свойству будет найдено применение.

Битонический сортировщик

Построим сеть, которая эффективно сортирует все битонические последовательности — т.н. битонический сортировщик.

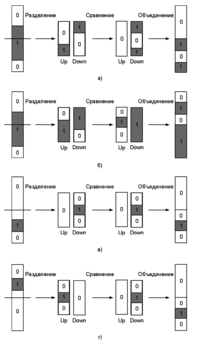
Полуфильтр Основной элемент битонического сортировщика называется полуфильтром (half-cleaner). Каждый полуфильтр — сравнивающая сеть единичной глубины, в которой [math]i[/math]-й входной провод сравнивается со входным проводом с номером [math]\frac{n}{2} + i[/math], где [math]i=1,2,...,\frac{n}{2}[/math] (пусть количество входов [math]n[/math] — чётное).

Рис.1 Полуфильтр для 8 проводов.

Лемма: Если на вход в полуфильтр подать битоническую последовательность из нулей и единиц длиной [math]n[/math], то на выходе мы получим две битонические последовательности длиной [math]\frac{n}{2}[/math] такие, что каждый элемент из верхней последовательности не превосходит любой элемент из нижней, и что одна из них будет однородной (clean) — целиком состоящей либо из нулей, либо из единиц. Доказательство: [math]\triangleright[/math] Для всех [math]i=1,2,...,\frac{n}{2}[/math] полуфильтр сравнивает провода с номерами [math]i[/math] и [math]i+\frac{n}{2}[/math]. Без потери общности будем рассматривать входную последовательность вида [math]0...01...10...0[/math] (для последовательности вида [math]1...10...01...1[/math] рассуждения аналогичны). В зависимости от того в каком блоке из последовательно расположенных нулей и единиц находится средняя точка [math]\frac{n}{2}[/math] входной последовательности, можно выделить 3 случая, причем один из случаев (когда средняя точка попадает на блок из единиц) можно разбить еще на 2 случая. Все 4 случая разобраны на рис. 2. Для каждого из них лемма выполняется. 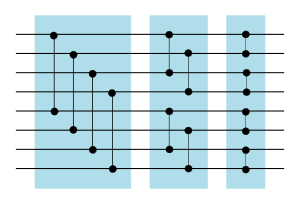[math]\triangleleft[/math] Построение битонического сортировщика Теперь используем полуфильтры для сортировки битонических последовательностей. Как только что было доказано, один полуфильтр разделяет битоническую последовательность на две равные части, одна из которых однородна, а другая сама по себе является битонической последовательностью, причем части расположены в правильном порядке. Тогда мы можем каждую часть снова отправить в полуфильтр вдвое меньшего размера, чем предыдущий. Затем, если нужно, четыре получившихся части снова отправить в полуфильтры и так далее, пока количество проводов в одной части больше [math]1[/math]. Схема битонического сортировщика для восьми входов приведен на рис. 3. Так можно построить сеть для числа входов, являющегося степенью двойки. Поскольку каждый вертикальный ряд полуфильтров вдвое сокращает число входов, которые необходимо отсортировать, глубина всей сети равна [math]\log_{2}n[/math], где [math]n[/math] — число входов. Количество компараторов равно [math]\frac{n \log_2{n}}{2}[/math], потому что размер одного полуфильтра на [math]n[/math] входов — [math]\frac{n}{2}[/math] компараторов, а в слое битонического сортировщика находится [math]2^{i-1}[/math] полуфильтров, где [math]i[/math] — номер слоя.

Рис.2 Все случаи попадания битонической последовательности на полуфильтр.

Объединяющая сеть

Битонический сортировщик находит своё применение в конструкции так называемой объединяющей сети.

Определение:

Объединяющая сеть (Merger) — сеть компараторов, объединяющая две отсортированные входные последовательности в одну отсортированную выходную последовательность.

Построим объединяющую сеть на основе битонического сортировщика. Для этого рассмотрим наши отсортированные входные последовательности:
Отсортированная последовательность имеет вид [math]0^i1^j[/math] для целых [math]i, j\ge0[/math]. Запишем две входные последовательности как [math]0^i1^j[/math] и [math]0^k1^l[/math]. Если перевернуть вторую последовательность, получится отсортированная по невозрастанию последовательность [math]1^l0^k[/math]. Если теперь записать первую и перевернутую вторую последовательности подряд, получится битоническая последовательность [math]0^i1^{j+l}0^k[/math], которую можно отсортировать в битоническом сортировщике с глубиной [math]O(\log{n})[/math].

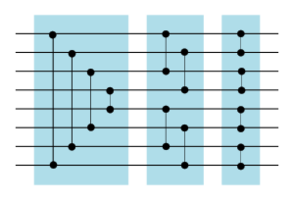
Объединяющая сеть является ничем иным как битоническим сортировщиком. Единственное отличие в том, что половина входных проводов расположена в обратном порядке (предполагается, что мы объединяем две сети одинакового размера [math]\frac{n}{2}[/math]). Поэтому первый полуфильтр будет отличаться от остальных — он будет соединять [math]i[/math]-ый провод не с [math]\frac{n}{2} + i[/math]-ым, а с [math]n-i+1[/math]-ым проводом. Схема объединяющей сети для восьми проводов приведена на рисунке 4.

Глубина и число компараторов в объединяющей сети очевидно те же, что и в битоническом сортировщике.

Сортирующая сеть

Построение

Теперь, с помощью описанных выше объединяющих сетей мы построим параллельную версию сортировки слиянием.
Пусть мы хотим отсортировать [math]n=2^k[/math] входов, [math]k[/math] — целое и [math]k \ge0[/math]. Для этого сначала отсортируем пары проводов, поставив в первом слое компаратор между [math]i[/math]-ым и [math]i+1[/math]-ым проводом для нечетных [math]i \lt n[/math]. Затем с помощью объединяющих сетей параллельно объединим отсортированные пары проводов в отсортированные четверки. Затем объединим отсортированные четверки в отсортированные восьмерки. И так далее, пока на выходе очередной объединяющей сети не будет [math]n[/math] проводов.
Схема такой сети приведена на рис. 5.

Рис.3 Битонический сортировщик на восемь входов с выделенными полуфильтрами.

Рис.4 Сеть, объединяющая две отсортированные последовательности из четырёх чисел в одну отсортированную последовательность из восьми чисел.

Рис.5 Сортирующая сеть для восьми проводов.

Точная глубина и размер сети

Оценим глубину этой сортирующей сети. Она состоит из [math]\log_2{n}[/math] слоёв объединяющих сетей, которые имеют глубину, зависящую от слоя. В слое с номером [math]i[/math] ([math]1 \le i \le \log_2{n}[/math]) объединяющие сети имеют глубину [math]\log_2{2^i}[/math], потому как объединяют [math]2^i[/math] проводов. Таким образом глубина всей сортирующей сети в точности равна [math]\sum\limits^{\log_2{n}}_{i = 1}{\log_2{2^i}} = \sum\limits^{\log_2{n}}_{i = 1}{i} = \frac{1+\log_2{n}}{2} \log_2{n}[/math].

Оценим размер сети. В объединяющей сети на [math]n[/math] входов содержится [math]\frac{n \log_2{n}}{2}[/math] компараторов. Снова просуммируем формулу по числу объединяющих сетей и получим точную оценку [math]\sum\limits^{\log_2{n}}_{i = 1}{ \frac{2^i \log_2{2^i}}{2} } = \sum\limits^{\log_2{n}}_{i = 1}{ 2^{i-1} i} = \frac{n \log_{2}^{2}{n} + 2 \log_2{n}}{4}[/math].

Источники

• Wikipedia — Batcher odd-even mergesort
• Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. — 2-е изд. — М.: Издательский дом «Вильямс», 2005. — С. 808—818.