Хеширование кукушки

Пример хеширования кукушки. Стрелки показывают второе возможное место элементов. Если нам надо будет вставить новый элемент на место А, то мы поместим А в его вторую ячейку, занятую В, а В переместим в его вторую ячейку, которая сейчас свободна. А вот помещение нового элемента на место Н не получится: так как Н — часть цикла, добавленный элемент будет вытеснен после прохода по циклу.

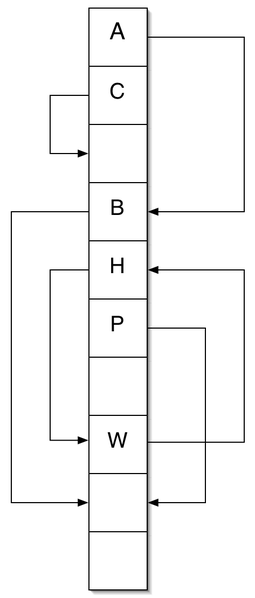
Хеширование кукушки — один из способов борьбы с коллизиями при создании хеш-таблицы.

Алгоритм

Основная идея хеширования кукушки — использование двух хеш-функций вместо одной (далее [math]h_1(x)[/math] и [math]h_2(x)[/math]). Также есть вариант алгоритма, в котором используются две хеш-таблицы, и первая хеш-функция указывает на ячейку из первой таблицы, а вторая — из второй. Рассмотрим алгоритмы функций add(x), remove(x) и contains(x).

Add — добавляет элемент с ключом [math]x[/math] в хэш-таблицу

1. Если одна из ячеек с индексами [math]h_1(x)[/math] или [math]h_2(x)[/math] свободна, кладем в нее элемент.
2. Иначе произвольно выбираем одну из этих ячеек, запоминаем элемент, который там находится, помещаем туда новый.
3. Смотрим в ячейку, на которую указывает другая хеш-функция от элемента, который запомнили, если она свободна, помещаем его в нее. Переходим к шагу 7.
4. Иначе запоминаем элемент из этой ячейки, кладем туда старый. Проверяем, не зациклились ли мы.
5. Если не зациклились, переходим к шагу 3.
6. Иначе выбираем 2 новые хеш-функции(из универсального семейства хэш-функций) и перехешируем все добавленные элементы.
7. Помечаем ячейку, в которую только что добавили элемент, как занятую.
8. Проверяем, если хэш-таблица заполнена увеличиваем её размер.

Remove — удаляет элемент с ключом [math]x[/math] из хэш-таблицы.

1. Смотрим ячейки с индексами [math]h_1(x)[/math] и [math]h_2(x)[/math].
2. Если в одной из них есть искомый элемент, просто помечаем эту ячейку как свободную.

Contains — проверяет на наличие элемента [math]x[/math] в хэш-таблице

1. Смотрим ячейки с индексами [math]h_1(x)[/math] и [math]h_2(x)[/math].
2. Если в одной из них есть искомый элемент, возвращаем true.
3. Иначе возвращаем false.

Зацикливание

Зацикливание может возникнуть при добавлении элемента. Пусть мы добавляем элемент [math]x[/math]. И обе ячейки [math]h_1(x)[/math] и [math]h_2(x)[/math] заняты. Пусть, элемент [math]x[/math] положили в ячейку [math]h_i(x)[/math]. Если в ходе перемещений элементов в таблице на очередном шаге мы опять хотим переместить элемент [math]x[/math] в ячейку [math]h_i(x)[/math], чтобы в ячейку [math]h_j(x) ~(i \ne j) [/math] поместить какой-то [math]y[/math] (это может произойти, если в ходе перемещений элемент [math]x[/math] был перемещен в ячейку [math]h_j(x)[/math]), то произошло зацикливание.

Например зацикливание возникнет если добавить в хэш-таблицу 3 элемента [math]x,y,z[/math] у которых [math]h_1(x)[/math] = [math]h_1(y)[/math] =[math]h_1(z)[/math] и [math]h_2(x)[/math] = [math]h_2(y)[/math] = [math]h_2(z)[/math] .

Время работы алгоритма

Удаление и проверка происходят за [math]O(1)[/math] (что является основной особенностью данного типа хеширования), добавление в среднем происходит за [math]O(1)[/math]. Первые два утверждения очевидны: требуется проверить всего лишь 2 ячейки таблицы.

Утверждение:

Добавление в среднем происходит за [math]O(1)[/math].

[math]\triangleright[/math]

Один из способов доказательства данного утверждения использует теорию случайных графов. Это делается через неориентированный "кукушкин граф", где каждой ячейке хеш-таблицы соответствует ровно одна вершина, а каждому добавленному элементу — ребро с концами в вершинах, соответствующих ячейкам, в которые указывают хеш-функции элемента. При этом элемент будет добавлен без перехеширования тогда и только тогда, когда после добавления нового ребра граф будет оставаться псевдолесом, то есть каждая его компонента связности будет содержать не более одного цикла.

[math]\triangleleft[/math]

Таким образом хеширование кукушки является одним из самых быстрых способов хеширования.

См. также

• Двойное хеширование

• Открытое и закрытое хеширование

Источники

• Wikipedia — Cuckoo hashing
• Cuckoo hashing — Pagh, Rasmus; Rodler, Flemming Friche (2001) (PDF, PS)