Материал из Викиконспекты
Определение
| Определение: |
Корреляция случайных величин: пусть [math]\eta,\xi[/math] — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их корреляция определяется следующим образом:
- [math]Corr(\eta,\xi)={Cov(\eta,\xi) \over \sigma_{\eta} \times \sigma_{\xi}}[/math].
|
Вычисление
Заметим, что [math]\sigma_{\xi} = \sqrt{D(\xi)} = E\big((\xi-E(\xi))^2\big)[/math]
- [math]Corr(\eta,\xi)={Cov(\eta,\xi) \over \sigma_{\eta} \times \sigma_{\xi}} = {E\big((\eta-E\eta)(\xi-E\xi)\big) \over {\sqrt{D(\eta)} \times \sqrt{D(\xi)}}} ={E(\xi \times \eta) - E(\xi) \times E(\eta) \over {\sigma_{\eta} \times \sigma_{\xi}}}[/math]
Свойства корреляции
| Утверждение: |
Корреляция симметрична:
- [math]Corr(\eta,\xi) = Corr(\xi,\eta)[/math].
|
| [math]\triangleright[/math] |
- [math]Corr(\eta,\xi) = { E(\eta \times \xi) - E(\eta) \times E(\xi) \over \sqrt{D(\eta)} \times \sqrt{D(\xi)} } = { E(\xi \times \eta) - E(\xi) \times E(\eta) \over \sqrt{D(\xi)} \times \sqrt{D(\eta)} } = Corr(\xi,\eta)[/math]
|
| [math]\triangleleft[/math] |
| Утверждение: |
Корреляция случайной величины с собой равна 1: |
| [math]\triangleright[/math] |
- [math]Corr(\eta,\eta) = { E(\eta \times \eta) - E(\eta) \times E(\eta) \over \sqrt{D(\eta)} \times \sqrt{D(\eta)} } = {D(\eta) \over D(\eta)} = 1[/math]
|
| [math]\triangleleft[/math] |
| Утверждение: |
Если [math]\eta,\xi[/math] независимые случайные величины, то
- [math]Corr(\eta,\xi) = 0[/math].
|
| [math]\triangleright[/math] |
|
Пусть [math]\eta[/math] и [math]\xi[/math] - независимые величины. Тогда [math]E(\eta \times \xi)=E(\eta) \times E(\xi)[/math], где [math]E[/math] - их математическое ожидание. Получаем:
- [math]{E(\xi) \times E(\eta) - E(\xi) \times E(\eta) \over {E\big((\eta-E(\eta))^2\big) \times E\big((\xi-E(\xi))^2\big)}} = 0[/math]
Но обратное неверно:
Пусть [math]\eta[/math] - случайная величина, распределенная симметрично около 0, а [math]\xi=\eta^2[/math]. [math]Corr(\eta,\xi)=0[/math], но [math]\eta[/math] и [math]\xi[/math] - зависимые величины. |
| [math]\triangleleft[/math] |
| Утверждение: |
Корреляция лежит не на всей вещественной оси
- [math]-1 \leqslant Corr(\eta,\xi) \leqslant 1[/math].
|
| [math]\triangleright[/math] |
|
Для доказательства используем свойство ковариации: [math]|Cov(\eta,\xi)| \leqslant \sqrt{D(\xi)} \cdot \sqrt{D(\eta)}[/math]. Тогда при раскрытии модуля получаем:
- [math]-\sqrt{D(\xi)} \cdot \sqrt{D(\eta)} \leqslant Cov(\eta,\xi) \leqslant \sqrt{D(\xi)} \cdot \sqrt{D(\eta)}[/math].
Поделим левую и правую части на [math]\sqrt{D(\xi)} \cdot \sqrt{D(\eta)}[/math] и получим: [math]-1 \leqslant {Cov(\eta,\xi) \over \sqrt{D(\xi)} \cdot \sqrt{D(\eta)}} \leqslant 1[/math], т.е.
- [math]-1 \leqslant Corr(\eta,\xi) \leqslant 1[/math], ч.т.д.
|
| [math]\triangleleft[/math] |
Примеры
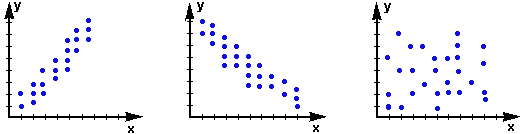
3 диаграммы рассеивания двух случайных величин X и Y
В общем смысле корреляция - это зависимость между случайными величинами, когда изменение одной влечет изменение распределения другой.
Определение корреляции по диаграмме
1. Соответственно, на первом графике изображена положительная корреляция, когда увеличение Y ведет к постепенному увеличению X.
2. Второй график отображает отрицательную корреляцию, когда увеличение Y воздействует на постепенное уменьшение X.
3. Третий график показывает, что X и Y связаны слабо, их распределение не зависит от изменения другой величины, поэтому корреляция между ними будет равна 0.
Ссылки
