Сортировочные сети с особыми свойствами

Нечетно-четная сортирующая сеть

Определение:

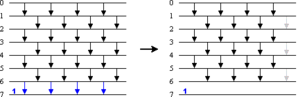
Нечетно-четная сортирующая сеть (odd-even sorting network) на [math]n[/math] входов [math]\lt a_1,a_2,...,a_n\gt [/math] — это транспозиционная сортирующая сеть с [math]n[/math] уровнями сравнивающих устройств, соединенных между собой по схеме "кирпичной кладки".

Примеры

Для [math]n=5[/math]	Для [math]n=6[/math] (Вариант 1)	Для [math]n=6[/math] (Вариант 2)

Как видно, из рисунка, при [math]i=1,2,...,n[/math] и [math]d=1,2,...,n[/math] линия [math]i[/math] соединена сравнивающим устройством на глубине [math]d[/math] c линией [math]j=i+(-1)^{i+d}[/math], если [math]1 \leqslant j \leqslant n[/math].

Так же вполне очевидно, что если [math]n[/math] четно, что имеется 2 варианта построения.

Одним из основных достоинств является то, что такую сортировку легко реализовать аппаратно, поскольку выполняются попеременно только 2 вида действий.

Теорема:

Нечетно-четная сортирующая сеть действительно является сортирующей сетью.

Докажем теорему методом математической индукции по [math]n[/math] линиям. Так же воспользуемся 0-1 принципом.

База индукции. При [math]n=1[/math] в сети не будет компараторов, но она очевидно будет являться сортирующей. Допустим, что наше предположение верно и для случая, где сеть имеет [math]n-1[/math] линий. Рассмотрим случай с [math]n[/math] линиями. Пусть на вход подается последовательность нулей и единиц: [math]a=a_0,...,a_{n-1}[/math]. Появляется 2 случая:

Случай 1. Если [math]a_{n-1}=1[/math], то компараторы [math][n-2:n-1][/math] ничего не изменят. И компараторы на линиях [math]\{0...n-1\}[/math] также не будет использовать [math]a_{n-1}[/math] элемент. По нашему предположению, наша сеть отсортирует последовательность [math]a_0,...,a_{n-2}[/math] длины [math]n-1[/math]. Итак, элемент a_{n-1} уже находится на правильной позиции, следовательно мы получим отсортированную последовательность [math]a[/math].

Случай 2. Если [math]a_{n-1}=0[/math], то этот элемент столкнувшись с любым компаратором будет совершать обмен (даже если обмен не является необходимым, когда другой элемент также [math]0[/math], результат будет таким же). Соответствующие компараторы могут быть замены путем скрещивания линий. По нашему предположению, наша сеть отсортирует последовательность [math]a_0,...,a_{n-2}[/math] длины [math]n-1[/math]. Итак, элемент [math]a_{n-1}[/math] путем прохождения сети будет помещен на правильную позиции, следовательно мы получим отсортированную последовательность [math]a[/math].

Перестановочная сеть

Определение:

Перестановочная сеть (permutation network) — сеть сортировки, содержащая на [math]n[/math] входов и [math]n[/math] выходов переключатели, позволяющие соединять входы сети с её выходами в соответствии с любой из [math]n![/math] возможных перестановок.

Определение:

Перестановочная сортирующая сеть (permutation sorting network) — сеть сортировки, содержащая последовательность компараторов [math][i_1:j_1]...[i_r:j_r][/math], где каждый модуль [i:j] может устанавливаться извне в одно из двух остояний: либо он передает свои входы без изменений, либо меняет местами [math]x_i[/math] и [math]x_j[/math] (независимо от значений [math]x_i[/math] и [math]x_j[/math])

Примеры

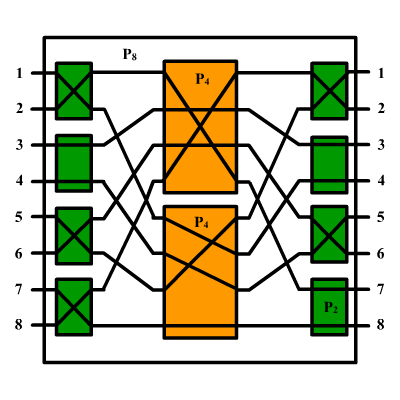На рисунке показана рекурсивная схема перестановочной сети [math]P_8[/math] на [math]8[/math] входов и [math]8[/math], которая содержит две копии [math]P_4[/math] и 8 переключателей ([math]P_2[/math]).

Периодическая сортировочная сеть

{{Определение |definition= Периодическая сортировочная сеть (periodic sorting network) на [math]n[/math] входов [math]\lt a_1,a_2,...,a_n\gt [/math] — сеть сортировки, содержащая [math]n = 2^t[/math] входов</tex>, где [math]t[/math] - уровень сети, и у которой каждый уровень может быть построен с помощью рекурсивного алгоритма.

Примеры

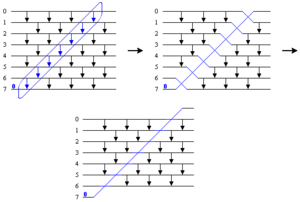
Для начала раскрасим все линии красным или синим цветом в соответствии со следующими правилами: Показанная на рисунке сеть следует считать иллюстрацией рекурсивного построения t-уровневой сети при [math]n=2^t[/math] в случае [math]t=4[/math]. Если пронумеровать линии входов от [math]0[/math] до [math]2^t-1[/math], то [math]l[/math]-й уровень имеет компараторы [math][i:j][/math], где [math]i \mod 2^{t+1-l} \lt 2^{t-l}[/math] и [math]j=i 0x (2^{t+1-l}-1)[/math]. Всего существует [math]t\cdot2^{t-1}[/math] компараторов, как и в сети битонного слияния.

Теорема:

Если входные числа [math]2^k[/math] - упорядочены при некотором [math]k \geqslant 1[/math], то периодическая сеть приведет к выходу, который будет [math]2^{k-1}[/math] - упорядочен.

Доказательство:

[math]\triangleright[/math]

Если [math]i \mod 4 = [/math] [math]0 \Rightarrow[/math] красный [math]1 \Rightarrow[/math] синий [math]2 \Rightarrow[/math] синий [math]3 \Rightarrow[/math] красный Теперь можно увидеть, что первые [math]t-1[/math] уровней сети состоят из двух отдельных сетей: одна из [math]2^{t-1}[/math] красных линий, а другая - из [math]2^{t-1}[/math] синих линий. Компараторы на [math]t[/math]-м уровне образуют сеть слияния, как в сетях битонного или четно-нечетного слияния. Таким образом, мы получили искомый результат при [math]k=1[/math]. Такой способ так же годится и для случая k=2. Если вход 4-упорядочен, красные линии содержат [math]2^{t-1}[/math] чисел, которые являются 2-упорядоченными; то же самое можно сказать относительно синих линий. Очевидно, что результат является 2-упорядоченным. Теперь для [math]k \geqslant 2[/math] можно предположить, что k<=t. Первые [math]t-k+2[/math] уровней разделяются на [math]2^{k-2}[/math] отдельных сетей размеров [math]2^{t-k+2}[/math], каждая из которых является [math]2[/math]-упорядоченной в случае [math]k=2[/math]; следовательно, линии являются [math]2^{k-1}[/math]-упорядоченными после [math]t-k+2[/math] уровней. Последующие уровни, очевидно, сохраняют [math]2^{k-1}[/math]-упорядоченность, так как они обладают "вертикальной" периодичностью порядка [math]2^{k-2}[/math].

[math]\triangleleft[/math]

Таким образом мы сможем сортировать [math]2^t[/math] чисел, пропуская их через сеть [math]t[/math] раз.

См. также

• Примитивные сортирующие сети
• Сортирующие сети для квадратичных сортировок

Ссылки

• Т. Кормен. «Алгоритмы. Построение и анализ» второе издание, Глава 27.5, стр. 819
• Д.Э. Кнут. «Искусство программирования: Сортировка и поиск" Том 3, Глава 5.3.4, стр. 275