F2Cmax
Содержание
Постановка задачи
Рассмотрим задачу:
- Дано работ и станка.
- Для каждой работы известно её время выполнения на каждом станке.
- Каждую работу необходимо выполнить сначала на первом станке, а потом на втором.
Требуется минимизировать время окончания всех работ.
Описание алгоритма
Пусть — время выполнения -ой работы на первом станке, а — на втором.
- Будем в ходе нашего алгоритма строить два списка и . Изначально оба списка пусты. И будем поддерживать множество еще не распределенных по спискам и работ
- Пока множество непусто будем распределять работы по спискам следующим образом:
- Находим такие индексы и , что
- Если минимум достигается на первом станке (иными словами ), то поставим работу в конец листа , иначе ставим в начало листа
- Удаляем работу из множества
- Рассмотрим лист . Утверждается, что этот лист является оптимальной перестановкой работ как на первом, так и на втором станке. Далее расставляем подряд работы на первом станке согласно перестановке, после чего ставим в том же порядке работы на втором стане, при этом избегая одновременного выполнения одной и той же работы.
Доказательство корректности алгоритма
| Теорема: |
Существует оптимальное расписание, в котором станки выполняют работы в одном и том же порядке. |
| Доказательство: |
|
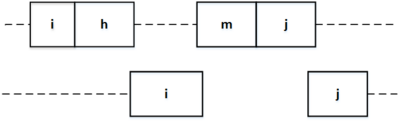
Предположим обратное, что не существует оптимального расписания с одиннаковыми перестановками работ на станках. Рассмотрим некоторое оптимальное расписание с максимальным по длине общим префиксом на станках. Пусть его длина равна , где . Пусть на позиций на первом и втором станках стоит работа , а на втором станке на позиций стоит работа . Тогда заметим, что если мы поставим работу на первом станке сразу после работы , то последовательные работы с по (см. Рис. 1) по-прежнему будут успевать выполниться, так как на втором станке они выполняются в текущем расписаний после . Таким образом нам удалось увеличить длину наибольщего общего префикса, а так как по нашему предположению она была максимальна, то наше предположение неверно, то искомое расписание с одиннаковым порядком выполнения работ на обоих станках существует. |
Таким образом задача сводится к поиску этой искомой перестановки. Докажем, что полученный нашим алгоритмом лист является отпимальной перестановкой работ.
| Лемма (1): |
Если для каких работ и из листа верно неравенство , то работа встречается в листе раньше, чем |
| Доказательство: |
|
Пусть . Случай рассматривается аналогично. То есть имеем, что . Так как , то работа . Работа либо стоит в , либо она стоит в и при этом . Заметим, что в обоих случаях она расположена позже (в силу нашего построения), чем работа , то лемма доказана. |
| Лемма (2): |
Пусть имеет случайное расписание, в котором работа идет сразу же после работы . Тогда если , то можем поменять местами эти работы без ухудшение целевой функций. |
| Доказательство: |
|
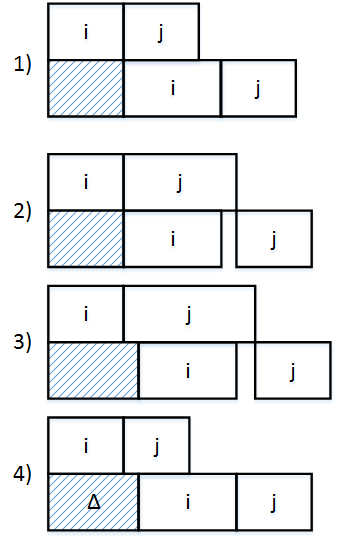
Пусть — время, прошедшее с начала выполнения работы на первом станке до окончания работы на втором станке. Рассмотрим возможные случаи расположения работ и (см. Рис. 2)
Таким образом, . Иначе говоря . Аналогично имеем, что Так как , то из условию леммы имеем , то добавим к обеим частям. То получим, что , то есть , то при смене местами работ и ответ не ухудшается. |
| Теорема: |
Построенная перестановка является оптимальной. |
| Доказательство: |
|
Рассмотрим случайную перестановку . Пусть перестановки и имеют общий префикс длины . Пусть и . Рассмотрим множество работ . Заметим, что для любой работы верно, что , так как если было бы верно обратное, то есть , то по Лемме 1 было бы верно, что идет раньше , что неверно. Очевидно, что в перестановке работа будет стоять после (иначе общий префикс был бы короче), то заметим, что в этой перестановке для работы и для предыдущей работы верно (так как ), то по Лемме 2 можем поменять местами работы и без ухудшения ответа. То такими операциями сможем дойти до пары работ и , которые при смене увеличат общий префикс перестановок и . Таким образом любая перестановка сводится к нашей без ухудшения ответа такими операциями, что подтверждает оптимальность перестановки |
Псевдокод
while Найти и , где if j = 1 else Расставляем работы на первом станке согласно перестановке Расставляем работы на втором станке согласно перестановке и времени начала соответсвующей работы на первом станке.
Сложность алгоритма
Заметим, что на каждом шаге алгоритма мы выбираем минимум из оставшихся элементов за (либо предварительной сортировкой, либо любой структурой данных, поддеживающей нахождение минимума и удаление за ). И делаем мы это раз, следовательно алгоритм работает за .
Источники
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 175 стр. — ISBN 978-3-540-69515-8