| Определение: |
Тройка [math]\langle G,\cdot, \varepsilon \rangle[/math] называется моноидом, если она удовлетворяет следующим аксиомам:
- Операция [math] \cdot \colon G \times G \rightarrow G [/math] ассоциативна.
- Существует нейтральный элемент [math] \varepsilon \in G [/math] относительно бинарной операции такой, что
- [math] \forall x\in G : \varepsilon\cdot x=x \cdot \varepsilon = x[/math]. Иногда его обозначают [math] \varepsilon_G [/math].
|
Другими словами, моноид — это полугруппа, в которую добавлен нейтральный элемент. Например, множество натуральных чисел с операцией сложения не является моноидом, а с операцией умножения — является.
| Утверждение (О единственности нейтрального элемента): |
Нейтральный элемент в моноиде единственен. |
| [math]\triangleright[/math] |
|
Действительно, пусть [math]\varepsilon_1[/math] и [math]\varepsilon_2[/math] — два нейтральных элемента. Тогда имеем: [math]\varepsilon_1 = \varepsilon_1\cdot \varepsilon_2 = \varepsilon_2[/math]. |
| [math]\triangleleft[/math] |
| Определение: |
| Гомоморфизмом моноидов (англ. monoid homomorphism) [math]M[/math] и [math]N[/math] называется отображение [math]\varphi \colon M \rightarrow N[/math] совместимое с операциями из [math] M [/math] и [math] N [/math] такое, что
[math] \forall m, m' \in M \colon \varphi(m\cdot m') = \varphi(m) \cdot \varphi(n)[/math], а также [math]\varphi(\varepsilon_M) = \varepsilon_N[/math]. |
| Определение: |
| Свободным моноидом (англ. free monoid) над множеством [math] S [/math] называется моноид [math] M [/math] вместе с отображением [math] i\colon S \rightarrow M [/math] при условии, что для любого моноида [math] N [/math] и для любых отображений [math] f \colon S \rightarrow N [/math] существует единственный гомоморфизм моноидов [math] \overline{f} \colon M(S) \rightarrow N [/math] такой, что [math] \overline{f} \circ i = f [/math]. |
Это наглядно показано следующей картинкой.
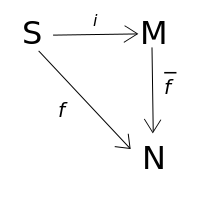
Если [math] S [/math] является подмножеством [math] M [/math], то отображение [math] i [/math] называют естественным вложением (англ. natural injection), и пишут [math] i \colon S \hookrightarrow M [/math].
Ссылки
