Материал из Викиконспекты
Лемма о разрастании[1](Pumping lemma) — лемма, позволяющая во многих случаях проверить, является ли данный язык регулярным.
| Лемма (о разрастании, о накачке): |
Пусть [math]L[/math] — регулярный язык над алфавитом [math]\Sigma[/math], тогда существует такое [math]n[/math], что для любого слова [math] \omega \in L[/math] длины не меньше [math]n[/math] найдутся слова [math] x,y,z \in \Sigma^*[/math], для которых верно: [math]xyz=\omega, y\neq \varepsilon, |xy|\leqslant n[/math] и [math]\forall k \geqslant 0~xy^{k}z\in L[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
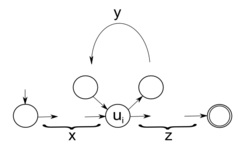
Пусть [math]L[/math] — регулярный язык над алфавитом [math]\Sigma[/math]. Поскольку регулярный язык является автоматным, то найдётся автомат [math]A[/math], допускающий язык [math]L[/math]. Пусть [math]n[/math] — размер автомата. Докажем, что [math]n[/math] удовлетворяет условию леммы.
Возьмём произвольное слово [math]\omega[/math] длины не меньше [math]n[/math] из языка [math]L[/math]. Рассмотрим переходы в автомате [math]\langle s,\omega\rangle \vdash\langle u_1, \omega[0]^{-1}\omega\rangle\vdash\dots\vdash\langle u_{l},\varepsilon\rangle, \: l\geqslant n[/math]. Так как [math]l[/math] не меньше количества состояний в автомате [math]n[/math], то в переходах будет совпадение. Пусть [math]u_i[/math] и [math]u_j[/math] — первое совпадение. Тогда, повторяя участок слова [math]\omega[/math], который отвечает за переход от [math]u_i[/math] к [math]u_j[/math], получаем слово, допускаемое автоматом. То есть, если верно [math]\langle s, xyz\rangle \vdash^*\langle u_i, yz\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math], то тогда верно [math]\langle s, xy^kz\rangle \vdash^*\langle u_i, y^kz\rangle\vdash^*\langle u_j, y^{k-1}z\rangle\vdash^*\langle u_j, z\rangle\vdash^*\langle u_l, \varepsilon\rangle[/math]. Тогда автомат [math]A[/math] допускает слово [math]xy^kz[/math], следовательно [math]xy^kz[/math] принадлежит регулярному языку [math]L[/math].
Наконец, поскольку [math]u_i[/math] и [math]u_j[/math] — первое совпадение, среди состояний [math]s, u_1, \ldots, u_i, \ldots, u_{j-1}[/math] нет повторяющихся. Значит, выполняется требование [math]|xy| \le n[/math]. |
| [math]\triangleleft[/math] |
Замечание. Условие леммы не является достаточным для регулярности языка. (См. пример)
Использование леммы для доказательства нерегулярности языков
Для доказательства нерегулярности языка часто удобно использовать отрицание леммы о разрастании. Пусть [math]L[/math] — язык над алфавитом [math]\Sigma[/math]. Если для любого натурального [math]n[/math] найдётся такое слово [math]\omega[/math] из данного языка, что его длина будет не меньше [math] n[/math] и при любом разбиении на три слова [math]x,y,z[/math] такие, что [math]y[/math] непустое и длина [math]xy[/math] не больше [math]n[/math], существует такое [math]k[/math], что [math]xy^kz \notin L[/math], то язык [math]L[/math] нерегулярный.
Рассмотрим такой подход на примере языка правильных скобочных последовательностей. Для фиксированного [math]n[/math] предъявляем слово [math]\omega=(^n)^n[/math]. Пусть [math]\omega[/math] как-то разбили на [math]x, y, z[/math]. Так как [math]|xy|\leqslant n[/math], то [math]y=(^b[/math], где [math]b \gt 0[/math]. Для любого такого разбиения берём [math]k=2[/math] и получаем [math]xy^kz=(^{n+b})^n[/math], что не является правильной скобочной последовательностью. Значит, язык правильных скобочных последовательностей нерегулярен.
Пример нерегулярного языка, для которого выполняется лемма о разрастании
Рассмотрим следующий язык: [math]L= \{ a^{i}b^{j}c^{k} \mid i \ge 2, j \ge 1, k \ge 1\} \cup \{ ab^{i}c^{i} \mid i \ge 1\}[/math]
Докажем, что он нерегулярный. Для этого рассмотрим вспомогательный язык [math]L'= \{ ab^{i}c^{i} \mid i \ge 1\}[/math] и докажем его нерегулярность. Воспользуемся предложенным в предыдущем пункте подходом. Для фиксированного [math]n[/math] выберем слово [math]\omega=ab^nc^n[/math]. Заметим, что при любом разбиении [math]\omega[/math] на [math]x, y, z[/math] слово [math] y [/math] не пусто (по условию леммы) и содержит только символы [math] a [/math] и [math] b [/math] (согласно выбранному слову и условию из леммы [math]|xy|\leqslant n[/math]). Это означает, что при [math] k = 0 [/math] слово [math]xy^kz[/math] либо не содержит символа [math] a [/math], либо количество символов [math] b[/math] меньше [math] n [/math]. В обоих случаях полученное слово не принадлежит языку. Значит язык [math] L' [/math] нерегулярный.
Предположим, что язык [math] L [/math] регулярный. Заметим, что [math]L' = L \cap \{ab^{*}c^{*}\} [/math]. В силу того, что пересечение регулярных языков регулярно, имеем в правой части равенства регулярный язык. При этом в левой части стоит язык, нерегулярность которого была доказана ранее. Значит наше предположение неверно, и язык [math] L [/math] нерегулярный.
Докажем, что язык удовлетворяет лемме о разрастании. Выберем в лемме [math] n = 2 [/math]. Это означает, что длина рассматриваемых слов не меньше [math] 2 [/math] (иными словами [math] i + j + k \ge 2 [/math]). Для каждого случая значений [math] i, j, k [/math] выберем соответствующие слова [math] x, y [/math] и [math] z [/math] из леммы. Легко проверить, что в каждом из приведенных ниже случаев условие леммы выполняется:
- [math] i = 1, j \ge 1, j = k [/math]. Слово имеет вид [math]\omega=ab^jc^j[/math]. Выберем [math] x = \varepsilon, y = a, z = b^jc^j[/math].
- [math] i = 2, j \ge 1, k \ge 1 [/math]. Слово имеет вид [math]\omega=aab^jc^k[/math]. Выберем [math] x = \varepsilon, y = aa, z = b^jc^k[/math].
- [math] i \ge 3, j \ge 1, k \ge 1 [/math]. Слово имеет вид [math]\omega=aaaa^{i-3}b^jc^k[/math]. Выберем [math] x = \varepsilon, y = a, z = aaa^{i-3}b^jc^k[/math].
Таким образом, язык [math] L [/math] удовлетворяет второй части леммы и при этом является нерегулярным, что доказывает тот факт, что лемма о разрастании не является достаточным для регулярности языка.
См. такжеПримечания
- ↑ Лемму также часто называют леммой о накачке.
Источники
