Квадродеревья

Эта статья находится в разработке!

Определение и построение

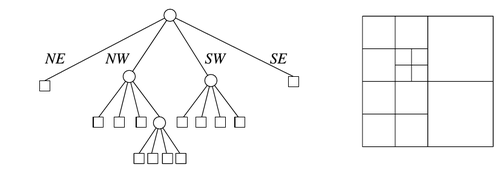
Квадродерево — дерево, каждая внутренняя вершина которого содержит 4 ребёнка. Любому узлу квадродерева соответствует некоторый квадрат. Если внутренней вершине [math]v[/math] соответствует какой-то квадрат [math]a[/math], то её детям соответствуют четверти квадрата [math]a[/math] (см. картинку).

По картинке должно быть понятно

Вообще говоря, квадродеревья могут быть использованы для разных целей и хранить разные данные, но нам они нужны для перечисления точек в произвольном прямоугольнике, соответственно, хранить в них будем какой-то набор точек.

Пусть дано множество точек [math]P[/math], для которого нужно построить квадродерево. Начнём с некоторого квадрата [math]\sigma[/math], содержащего все точки из [math]P[/math]. Если он не дан явно, его можно легко найти за линейное время от числа вершин. Пусть [math]\sigma = [x_0, x_1] \times [y_0, y_1][/math]. Обозначим [math]x_m = (x_0 + x_1) / 2; y_m = (y_0 + y_1) / 2[/math]. Тогда:

• если [math]P[/math] содержит не больше одной точки, то квадродерево состоит из одного листа, которому соответствует квадрат [math]\sigma[/math];
• иначе корнем дерева делаем вершину [math]v[/math], которой соответствует квадрат [math]\sigma[/math], а его дети — [math]v_{NE}, v_{NW}, v_{SW}, v_{SE}[/math], и им соответствуют квадраты [math]\sigma_{NE} = (x_m, x_1] \times (y_m, y_1][/math], [math]\sigma_{NW} = [x_0, x_m] \times (y_m, y_1][/math], [math]\sigma_{SW} = [x_0, x_m] \times [y_0, y_m][/math], [math]\sigma_{SE} = (x_m, x_1] \times [y_0, y_m][/math]. Затем таким же образом рекурсивно превращаем каждого ребёнка в квадродерево для множества точек, лежащих в соответствующем квадрате.

Леммы и теоремы

Сперва оценим глубину квадродерева. Если какие-то две точки лежат очень близко, то процесс построения может продолжаться очень долго, поэтому глубину невозможно оценить функцией от числа вершин.

Лемма:

Глубина квадродерева для множества точек [math]P[/math] не превосходит [math]log(s / c) + 3/2[/math], где [math]c[/math] — наименьшее расстояние между двумя точками из [math]P[/math], а [math]s[/math] — сторона квадрата, с которого начинается построение квадродерева.

Доказательство:

[math]\triangleright[/math]

Сторона квадрата на глубине [math]i[/math], очевидно, равна [math]s / 2^i[/math]. Максимальное расстояние между двумя точками внутри квадрата достигается, когда они являются вершинами диагонали, то есть на глубине [math]i[/math] расстояние между любыми двумя точками в одном квадрате не превосходит [math]s \sqrt 2 / 2^i[/math]. Поскольку внутренняя вершина квадродерева содержит хотя бы 2 точки в соответствующем ей квадрате, то [math]s \sqrt 2 / 2^i \geq c[/math], так как [math]c[/math] — минимальное расстояние между точками в [math]P[/math]. Отсюда следует, что [math]i \leq log(s \sqrt 2 / c) = log (s / c) + 1/2[/math]. Значит, глубина любой внутренней вершины не превосходит [math]log (s / c) + 1/2[/math], из чего следует утверждение леммы.

[math]\triangleleft[/math]

Размер дерева и время построения будут также зависеть и от [math]n[/math] — мощности [math]P[/math].

Теорема:

Квадродерево глубины [math]d[/math] для [math]n[/math] точек содержит [math]O(d \cdot n)[/math] вершин и может быть построено за [math]O(d \cdot n)[/math].

Доказательство:

[math]\triangleright[/math]

Поскольку каждая внутренняя вершина имеет четырёх детей, то суммарное число листьев будет [math]3i + 1[/math], где [math]i[/math] — число внутренних вершин. Поэтому достаточно доказать, что внутренних вершин [math]O(d \cdot n)[/math]. Каждая внутренняя вершина содержит хотя бы одну точку в соответствующем ей квадрате. Заметим, что квадраты с одного уровня не пересекаются и полностью покрывают весь исходный квадрат (в котором [math]n[/math] точек). Значит, число внутренних вершин одного уровня не может первосходить [math]n[/math]. Из этого следует, что всего внутренних вершин [math]O(d \cdot n)[/math].

[math]\triangleleft[/math]

Литература

• van Kreveld, de Berg, Overmars, Cheong — Computational Geometry. Algorithms and Applications. Страница 309.