Выпуклая оболочка в n-мерном пространстве

Конспект написан не до конца, но основные вещи уже есть.

Рассмотрим трёхмерный случай. [math]n[/math]-мерный сводится к трёхмерному.

Суть алгоритма

Выберем любые две точки [math]p_1[/math] и [math]p_2[/math]. Далее из оставшихся выберем точку [math]p_3[/math], которая не лежит на прямой, образованной точками [math]p_1[/math] и [math]p_2[/math]. После этого выберем точку [math]p_4[/math], которая не лежит на плоскости, образованной точками [math]p_1, p_2[/math] и [math]p_3[/math]. Если этого сделать не получилось, то запустим алгоритм для поиска выпуклой оболочки на плоскости.

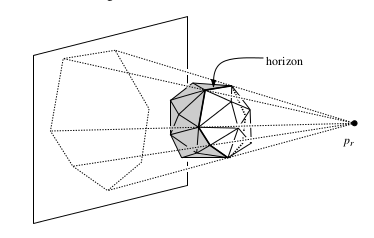
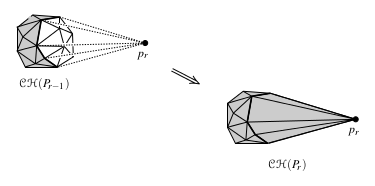
Так мы получили тетраэдр [math]p_1 p_2 p_3 p_4[/math], который является выпуклой оболочкой этих четырёх точек. Сделаем random shuffle оставшихся точек [math]p_5, ..., p_n[/math] и будем добавлять их по одной в выпуклую оболочку. Если [math]p_i[/math] внутри или на границах выпуклой оболочки, то выпуклая оболочка не меняется на этом шаге. Иначе из имеющейся выпуклой оболочки надо удалить все видимые из данной точки грани и добавить новые — из точки до каждого ребра, образующего horizon (см. картинки; на них белые грани видны из точки [math]p_r[/math]). После этого нужно смержить соседние грани, которые получились копланарными.

Детали реализации

Будем хранить выпуклую оболочку в виде DCEL.

Для выяснения, какие грани видны из точки, будем хранить двудольный граф [math]G[/math], называемый conflict graph, в одной доле которого будут точки, которые ещё не добавлены в выпуклую оболочку, а в другой — имеющиеся на данный момент грани выпуклой оболочки. Ребро между точкой [math]p[/math] и гранью [math]f[/math] в этом графе означает, что из [math]p[/math] видна [math]f[/math], то есть они находятся в конфликте (in conflict): они не могут сосуществовать в выпуклой оболочке.

Инициализация графа для тетраэдра тривиальна: для каждой точки определяем, какие грани видны из неё. Далее на каждом шаге после добавления точки [math]p_r[/math] удалим из графа соответствующие удаляемым из выпуклой оболочки граням вершины и инцидентные им рёбра: просто удаляем все достижимые из [math]p_r[/math] вершины. Также удалим вершину, соответствующую [math]p_r[/math]. Далее добавляем новые грани выпуклой оболочки. Необходимо найти их конфликты. Сами грани представляют из себя треугольники, если, конечно, они не были смержены с уже имеющимися гранями. Во втором случае новая грань находится в конфликте с теми же точками, что и старая грань, т.к. смерженные грани копланарны.

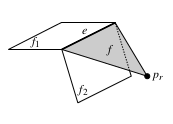
Перейдём к первому случаю. Пусть мы добавили точку [math]p_r[/math] и рассматриваем грань [math]f[/math]. [math]e[/math] — ребро, принадлежащее horizon, [math]f_1, f_2[/math] — грани, пересечение которых образовывало [math]e[/math] в старой оболочке. Пусть [math]p_t[/math] — ещё не добавленная точка, из которой видно [math]f[/math], тогда из неё видно и ребро [math]e[/math], причём как в новой, так и в старой выпуклой оболочке (так как новая включает в себя старую). Но это возможно, только если из [math]p_t[/math] видно [math]f_1[/math] или [math]f_2[/math]. Значит, точки, с которыми у [math]f[/math] есть конфликт — это только какие-то из точек, у которых есть конфликт у [math]f_1[/math] и [math]f_2[/math].

Время работы

Лемма (1):

Пусть [math]P[/math] — выпуклый многогранник с [math]n[/math] вершинами. Тогда число его рёбер не превосходит [math]3n - 6[/math], а число его граней — [math]2n - 4[/math].

Доказательство:

[math]\triangleright[/math]

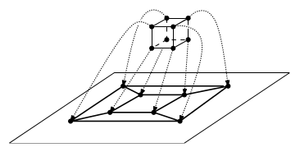
Верхняя грань куба спроецировалась на внешнюю грань графа «Спроецируем» многогранник на плоскость, как на картинке. Получили планарный граф, по формуле Эйлера имеем [math]n - n_e + n_f = 2[/math], где [math]n_e[/math] — число рёбер, [math]n_f[/math] — число граней. Каждая грань нашего графа имеет по меньшей мере 3 ребра, каждое ребро инцидентно двум граням, поэтому имеем [math]2 n_e \geqslant 3 n_f[/math]. Тогда получаем [math]n_f \leqslant 2n - 4[/math], и, подставив это в формулу Эйлера, [math]n_e \leqslant 3n - 6[/math].

[math]\triangleleft[/math]

Лемма (2):

Ожидаемое число граней, создаваемое нашим алгоритмом, не превосходит [math]6n - 20[/math].

Доказательство:

[math]\triangleright[/math]

Рассмотрим добавление точки [math]p_r[/math]. Все грани, добавленные на этом шаге алгоритма, инцидентны этой точке, равно как и добавленные рёбра. Обозначим число инцидентных точке [math]p_i[/math] рёбер (степень вершины; оно же число инцидентных точек) в выпуклой оболочке [math]r[/math] точек как [math]k_{i, r}[/math]. По лемме 1 у многогранника с [math]r[/math] веришнами не больше [math]3r - 6[/math] рёбер. Значит, сумма степеней вершин многогранника не больше [math]6r - 12[/math]. Значит, средняя степень вершины равна [math]6 - 12/r[/math]. Точки берутся в случайном порядке, поэтому можно считать, что ожидаемая степень вершины [math]p_r[/math] равна [math]6 - 12/r[/math]. Это рассуждение верно только для [math]r \gt 4[/math], так как первые четыре точки фиксированы, их суммарная степень равна [math]12[/math]. Посчитаем математическое ожидание [math]k_r[/math]: [math]E(k_{r, r}) = \frac{1}{r - 4} \sum_{i = 5}^{r} k_{i, r} \leqslant \frac{1}{r - 4} ( \sum_{i = 1}^{r} k_{i, r} - 12 ) \leqslant \frac{6r - 12 - 12}{r - 4} = 6[/math]. Ожидаемое число граней — это число граней в начальном тетраэдре (4 — ваш К.О.) плюс ожидаемое общее число созданных граней при добавлении точек. Поэтому искомое число равно [math]4 + \sum_{r = 5}^{n} E(k_{r, r}) \leqslant 4 + 6(n - 4) = 6n - 20[/math].

[math]\triangleleft[/math]