Пересечение многоугольников (PSLG overlaying)

Input [math]\Rightarrow[/math] Output

Создание новой компоненты

Создание новой компоненты

Граф для поиска face

Постановка задачи

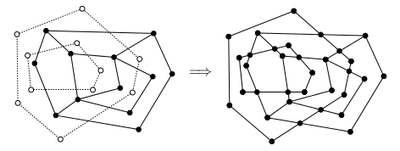
Даны два ППЛГ, требуется построить их объединение в виде РСДС. При этом создав новые [math]face[/math] и обновив старые.

Формально

Определим объединение двух pslg [math]S1[/math] и [math]S2[/math], чтобы получился граф [math]O(S1, S2)[/math], такой, что существует [math]face[/math] f в [math]O(S1, S2)[/math], тогда и только тогда есть [math]face[/math] f1 и f2 в [math]S1[/math] и [math]S2[/math] соответственно, что [math]f[/math] является максимально связанным подмножеством [math]f1 \cap f2[/math]. Требуется чтобы каждый [math]face[/math] в [math]O(S1, S2)[/math] был отмечен с помощью label of the [math]faces[/math] в [math]S1[/math] и [math]S2[/math], который содержит их. Таким образом мы получаем доступ к информации хранящейся на этих [math]faces[/math].

Алгоритм

Первоначальное слияние

Для начала посмотрим, как можно больше информации от doubly connected edge lists для [math]S1[/math] и [math]S2[/math] мы можем повторно использовать в doubly connected edge lists для [math]O(S1, S2)[/math]. Рассмотрим сеть ребер и вершин S1. Эта сеть разделена на кусочки краями [math]S2[/math]. Эти кусочки в большинстве своем могут использоваться повторно, все, за исключением тех, которые отделены краями [math]S2[/math]. Такие нужно обновлять. Если ориентация [math]half-edge[/math] изменится, нам придется менять информацию в этих записях. Половинки ребра ориентированы таким образом, что [math]face[/math], которым они связаны лежит слева; форма [math]face[/math] может изменяться в наложении, но он будет оставаться в той же стороне [math]half-edge[/math]. Следовательно, мы можем повторно использовать [math]half-edge[/math] records, соответствующие краям, которые не пересекают ребра из другого графа.

Объединения графов

Во-первых, скопировать doubly­ connected edge lists [math]S1[/math] и [math]S2[/math] в один новый [math]DCEL[/math]. Новый [math]DCEL[/math] не является допустимым [math]DCEL[/math], т.к. он еще не представляет собой плоский подграф. Это задача алгоритма заметающей прямой: он должен трансформировать [math]DCEL[/math] в допустимый [math]DCEL[/math] для [math]O(S1, S2)[/math] путем вычисления пересечения между двумя сетями ребер, и связывая воедино соответствующие части из двух [math]DCEL[/math]. Применяем этот алгоритм на множестве сегментов, что является объединением множеств ребер двух подграфов [math]S1[/math] и [math]S2[/math]. Алгоритм поддерживается двумя структурами данных: очереди событий [math]Q[/math], в котором хранятся точки событий, и структура состояния [math]T[/math], которой является бинарное дерево храненящее сегменты, пересекающие линии развертки, расположенные слева направо. Мы теперь также должны поддерживать [math]DCEL[/math] [math]D[/math]. Первоначально [math]D[/math] содержит копию [math]DCEL[/math] для [math]S1[/math] и [math]DCEL[/math] для [math]S2[/math]. В плоскости развертки преобразуем [math]D[/math] к правильному [math]DCEL[/math] для [math]O(S1, S2)[/math]. Мы держим перекрестные указатели между ребер в структуре состояния [math]T[/math] и половина текущих записей в [math]D[/math], которые соответствуют им. Таким образом мы можем получить доступ к части [math]D[/math], которая должна быть изменена, когда мы сталкиваемся с точкой пересечения.

В другом случае, мы поддерживаем то, что в любое время в течение развертки, часть выше линии развертки наложения будет считаться правильной. Теперь что мы должны делать, когда мы достигнем точки событий. Прежде всего, мы обновляем [math]T[/math] и [math]Q[/math], как и в алгоритме заметающей прямой. Если событие включает в себя только ребра из одного из двух подграфов, это все, точка событие является вершиной, которые могут быть использованы повторно. Если событие включает края с двух подграфов, мы должны сделать локальные изменения в [math]D[/math] -- связать doubly­ connected edge list двух оригинальных подграфов в точке пересечения.

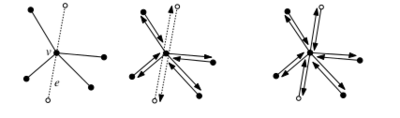
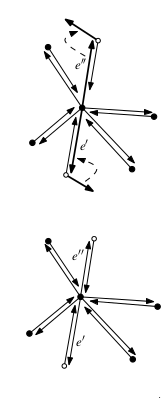
Рассмотри, когда edge [math]e[/math] из [math]S1[/math] проходит через вершину [math]V[/math] [math]S2[/math], (см. Рисунок) edge [math]e[/math] должно быть заменено двумя edges обозначим [math]e'[/math] и [math]e''[/math]. В [math]DCEL[/math], два [math]half-edge[/math] для е должны превратиться в четыре. Мы создаем два новых [math]half-edge[/math], с [math]V[/math] в нуле. Два существующих [math]half-edge[/math] для е содержат конечные точки [math]e[/math], как их происхождения. Тогда мы объединяем попарно существующие [math]half-edges[/math] с новыми [math]half-edges[/math], устанавливая их указатели twin'ов. Так [math]e'[/math] представлен одним новым и одним существующим частично edge, и то же самое для [math]e''[/math]. Теперь мы должны установить [math]Prev[/math] и [math]Next[/math]. [math]Next[/math] двух новых [math]half-edges[/math] являются копией [math]Next[/math] старого [math]half-edge[/math], не имеющего пары. В [math]half-edges[/math], в которые эти указатели точки должны обновлять свои [math]Prev[/math] и устанавливать его на новых [math]half-edges[/math]. Далее мы должны установить [math]Next[/math] и [math]Prev[/math] четырех [math]half-edges[/math] представляющих [math]e'[/math] и [math]e''[/math], и из четырех [math]half-edges[/math] инцидентного [math]S2[/math] [math]v[/math]. Мы размещаем эти четыре [math]half-edges[/math] от [math]S2[/math], проверяя, где [math]e'[/math] и [math]e''[/math] должны быть в циклическом порядке вершин вокруг вершины [math]v[/math]. Есть четыре пары [math]half-edges[/math], которые связанны между собой [math]Next[/math] с одним и [math]Prev[/math] с другим. [math]e'[/math] должен быть привязан к первому [math]half-edge[/math] по часовой стрелке с началом в [math]v.[/math] [math]half-edge[/math] для [math]e'[/math] с началом в [math]v[/math] должен быть связан с первым против часовой стрелки [math]half-edge[/math] с окончанием в [math]v[/math]. Точно также и для [math]e''[/math].

Время работы объединения

Большинство из шагов в приведенном выше описании принимать только константное время. Есть случаи на которые потребуется дополнительное время, О(M), где M­число ребер, точки событий. Это означает, что обновление [math]D[/math] не увеличивает время работы алгоритма заметащей прямой асимптотически. Любое пересечение, которое мы находим является вершиной наложения. Из этого следует, что вершина record и [math]half-edge[/math] record doubly­ connected edge list для [math]O(S1, S2)[/math] можно вычислить за [math]O(n \ * \ \log n + k \ *\ \log n)[/math] время, где [math]n[/math] обозначает сумму сложностей [math]S1[/math] и [math]S2[/math], а k является сложностью наложения.

Воссоздание [math]faces[/math]

После того, как все сделано, осталось вычислить информацию о [math]faces[/math] в [math]O(S1, S2)[/math]. Точнее, мы должны создать [math]face[/math] record для каждого [math]face[/math] е в [math]O(S1, S2)[/math], мы должны сделать [math]outer\_component[/math] ([math]e[/math]) указывают на [math]half-edges[/math] на внешней границе [math]F[/math], и мы должны сделать список [math]inner\_components[/math] ([math]F[/math]) из указателей на [math]half-edges[/math] на связанных областях пробелов внутри [math]f[/math]. Кроме того, мы должны установить [math]incident\_face[/math] () поля времени [math]half-edges[/math] на границе [math]F[/math] так, что они указывают на лицевые записи [math]F[/math]. Наконец, каждый из новых [math]faces[/math] должны быть помечены именами [math]faces[/math] в старых подграфах, которые содержат его. Рассмотрим два [math]half-edges[/math] цикла, свойственных [math]v[/math]. Т.к. мы знаем, что incident [math]face[/math] лежит слева, мы можем вычислить угол который эти два [math]half-edges[/math] образуют внутри [math]face[/math]. Если этот угол f меньше, чем 180◦ то циклом является внешняя граница, и в противном случае это граница дыры. Это свойство имеет место для левой вершины цикла, но не обязательно для других вершин этого цикла.

Лемма (К предыдущему вопросу):

Каждая компонента графа отвечает за множество циклов инцидентных одному [math]face[/math].

Доказательство:

[math]\triangleright[/math]

Рассмотрим цикл [math]C[/math], который ограничивает дыру в [math]face[/math] [math]f[/math]. Поскольку [math]f[/math] локально лежит левее самой левой вершины из [math]C[/math], то [math]C[/math] должен быть соединен с другим циклом, который тоже ограничивает [math]f[/math]. отсюда следует, что циклы есть компонента связности в графе, описывающая один и тот-же [math]face[/math]. Для того, что бы закончить доказательство, покажем, что каждый цикл ограничивающий дыру в [math]f[/math] есть в той же компоненте связности, что и внешняя граница [math]f[/math]. Предположим, что есть цикл, для которого это не так. Пусть [math]C[/math] — самый левый такой цикл, то есть тот, чья самая левая вершина самая левая. По определению есть ребро между [math]C[/math] и неким [math]C'[/math], который лежит слева от самой левой вершины [math]C[/math]. Следовательно [math]C[/math] в той же компоненте связности, что и [math]C'[/math], который не в той же компоненте, что внешняя граница [math]f[/math]. Противоречие.

[math]\triangleleft[/math]

Напомним, что в алгоритме развертки плоскости для отрезка пересечения мы всегда искали сегменты сразу слева от точки событий. (Они должны были быть проверены на пересечении с крайнего левого края через точку событий.) Таким образом, информация, при помощи которой мы должны построить [math]G[/math] определяется в плоскости развертки. Таким образом, чтобы построить [math]G[/math], мы сначала делаем узел для каждого цикла. Чтобы найти дуги [math]G[/math], рассмотрим левую вершину [math]V[/math] для каждого цикла, ограничивающую отверстие. Если [math]half-edge[/math] сразу же выходит из [math]V[/math], то мы добавляем дугу между двумя узлами в [math]G[/math], представляющих цикл, содержащий е и цикл у которого [math]V[/math] является самой левой вершиной. Чтобы найти эти узлы в [math]G[/math] мы должны указатели от каждого [math]half-edge[/math] записать в узел [math]G[/math], представляющего цикл этот. Так информация o [math]face[/math] в doubly­connected edge list может быть установлена в [math]О(n\ +\ k)[/math] времени, после плоскости развертки. Каждая грань [math]e[/math] в наложении должна быть помечена с именами [math]face[/math] в старых графах, которые содержали его. Чтобы найти эти [math]face[/math], надо рассмотреть произвольную вершину [math]V[/math] в [math]F[/math]. Если [math]v[/math] является пересечением [math]e1[/math] от [math]S1[/math] и [math]е2[/math] от [math]S2[/math], то мы можем решить, какие [math]face[/math] из [math]S1[/math] и [math]S2[/math] содержат [math]F[/math], глядя на [math]incident\_face[/math] указатель соответствующих [math]half-edges[/math] соответствующих [math]e1[/math] и [math]e2[/math]. Если [math]v[/math] не пересечение, но вершина, скажем, S1, то мы знаем только [math]face[/math] S1, содержащей [math]f[/math]. Чтобы найти [math]face[/math] [math]S2[/math] , содержащий [math]F[/math], мы должны определить [math]face[/math] [math]S2[/math], которое содержит [math]v[/math]. Другими словами, если бы мы знали для каждой вершины [math]S1[/math], в котором [math]face[/math] [math]S2[/math] находился, и наоборот, то мы могли бы обозначить [math]face[/math] [math]O(S1, S2)[/math] правильно.

Итог

MapOverlay ([math]S_1[/math], [math]S_2[/math]) [math]:[/math]

1. Копируем [math]S_1[/math] и [math]S_2[/math] в граф [math]D[/math].

2. Находим все пересечения ребер из [math]S_1[/math] с ребрами из [math]S_2[/math] с помощью заметающей прямой.

2.1 Когда находим точки пересечения, то обновляем [math]D[/math], то есть строим из него РСДС.

3. Теперь [math]D[/math] это нормальный РСДС, но без информации о [math]face[/math]'ах.

4. Находим boundary cycles в [math]D[/math]. То есть обновляем этот граф. Пока только добавляя в него ребра ([math]half-edge[/math]'ы соответственно).

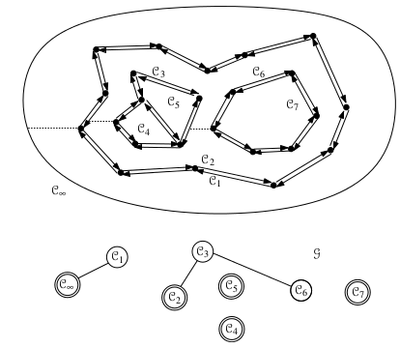
5. Создаем граф [math]G[/math] (о нем ниже), в котором узлы будут отвечать за boundary cycles и в котором ребра будут соединять только те узлы, один из которых будет являться границей дыры ([math]hole[/math], это внутренний цикл [math]face[/math]'a), а другой будет находиться слева от самой левой точки первого. (В случае, если это самая внешняя граница, то для нее пусть будет мнимая гигантская граница, с которой мы ее и соединим).

5.1. Для каждой компоненты графа:

Пусть [math]C[/math] будет уникальная наружная граница цикла в компоненте, а [math]f[/math] будет означать face ограниченный этим циклом. Создадим face для [math]f[/math]. Запишем [math]outer\_component[/math] в какой-нибудь [math]half-edge[/math] из [math]C[/math]. И создадим список [math]inner\_components[/math], состоящий из указателей на какой-нибудь [math]half-edge[/math] из каждого цикла. А так же пусть [math]incident\_face[/math] в каждом [math]half-edge[/math] будут обновлены на [math]f[/math].

Литература и источники

• Вычислительная геометрия. Алгоритмы и приложения, де Берг Марк и другие. Глава 2.3