Двоичный каскадный сумматор
Версия от 05:07, 15 октября 2010; Tanfilyev (обсуждение | вклад)
Эта статья находится в разработке!
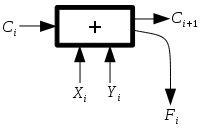
Рассмотрим один элемент полного сумматора:
Построим таблицу зависимости от , и введем условные обозначения:
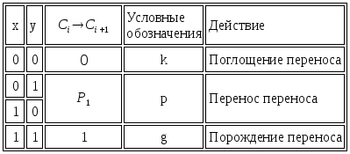
Обозначим композицию действий над переносами значком и рассмотрим таблицу:
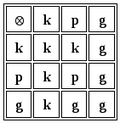
Пример:
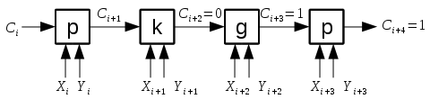
Таким образом функцию можно определить как последнее не "P"
Пусть , тогда: .
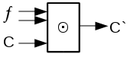
Пусть элемент
возвращает двух функций, а
Возврощает , старший бит сумматора.
dd