Cумматор

Сумматор (англ. adder) — логический операционный узел, выполняющий арифметическое сложение двоичных, троичных или [math]n[/math]-ичных кодов. Может складывать два (бинарный), три (тернарный) или [math]n[/math] чисел ([math]n[/math]-арный). Помимо сложения выполняются и другие операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное.

Неполный сумматор

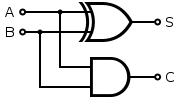
Неполный сумматор (англ. half adder) — логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Позволяет вычислять сумму [math]A+B[/math], где [math]A[/math] и [math]B[/math] — это разряды двоичного числа. При этом результатом будут два бита [math]S[/math] и [math]C[/math], где [math]S[/math] — это бит суммы по модулю [math]2[/math], а [math]C[/math] — бит переноса. [math]S = A \oplus B[/math], [math]C = A \wedge B[/math], [math]A + B = 2 \times C + S[/math].

Полный сумматор

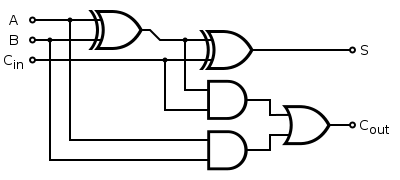
Полный сумматор (англ. full adder) — логическая схема, которая производит сложение трех битов, часто обозначаемых [math]A[/math], [math]B[/math] и [math]C_\mathrm{in}[/math]. На выход подаются два бита [math]S[/math] и [math]C_\mathrm{out}[/math], где [math]S[/math] — это бит суммы по модулю, а [math]C_\mathrm{out}[/math] — бит переноса. [math]C_\mathrm{out} = \bigl\langle A , B , C \bigr\rangle[/math], [math]S = A \oplus B \oplus C[/math], [math]A + B + C = 2 \times C_\mathrm{out} + S[/math].
Полный сумматор используется при построении двоичного каскадного сумматора.

См. также

• Реализация булевой функции схемой из функциональных элементов
• Изменение размера оптимальной схемы при переходе к другому базису
• Каскадный сумматор
• Двоичный каскадный сумматор
• Матричный умножитель
• Дерево Уоллеса

Литература

• Угрюмов Е. П. Элементы и узлы ЭЦВМ. М.: Высшая школа, 1976. — 232 с.
• Угрюмов Е. П. Цифровая схемотехника. — СПб.: БХВ-Петербург, 2001. — 528 с.
• Жан М. Рабаи, Ананта Чандракасан, Боривож Николич. 11. Проектирование арифметических блоков: Сумматор // Цифровые интегральные схемы. Методология проектирования = Digital Integrated Circuits. — 2-е изд. — М.: Вильямс, 2007. — С. 912. — ISBN 0-13-090996-3