Теорема Понтрягина-Куратовского
Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2
Рассмотрим 2 случая.
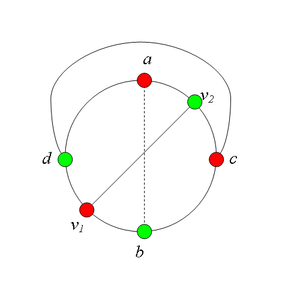
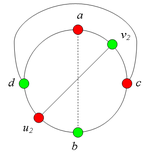
1. Пусть пара вершин и является -разделяющей.
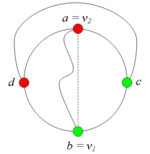
Тогда, в частности, и . В этом случае граф G содержит подграф, гомеоморфный (отметим, что в существует простая -цепь)(рис. 1).
2. Пусть пара вершин и не является -разделяющей.
Тогда лежат на или на . Без ограничения общности будет считать, что и лежат на .
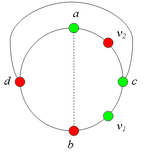
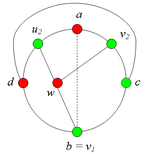
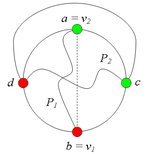
2.1. Пусть и лежат на , т.е. и (рис. 2).
2.1.1 Пусть лежит на .
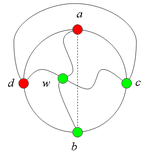
Тогда в графе G имеется подграф, гомеоморфный (рис. 3).
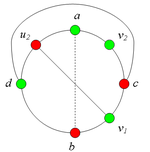
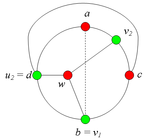
2.1.2. Пусть .
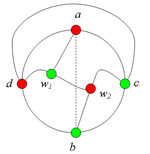
Тогда во внешней части имеется вершина и три простые цепи от соответственно до , которые в качестве общей точки имеют только точку . В этом случае в графе G имеется подграф, гомеоморфный (рис. 4).
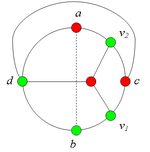
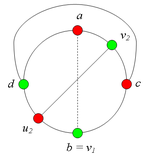
2.1.3. Пусть лежит на .
Тогда в графе G есть подграф, гомеоморфный (рис. 5).
Теперь рассмотрим случаи, когда хотя бы одна из вершин и не лежит на . Без ограничения общности будем считать, что это вершина , т.е (поскольку лежит на ).
2.2. Пусть .
2.2.1. Пусть лежит на .
Тогда в графе G есть пограф, гомеоморфный (рис. 6).
2.2.2. Пусть .
Тогда в графе G имеется подграф, гомеоморфный (рис. 7).
2.2.3. Пусть лежит на .
Тогда в графе G имеется подграф, гомеоморфный (рис. 8).
2.3. Пусть (рис. 9).
Рассмотрим теперь пару вершин и . Будем считать, что и , поскольку все другие случаи расположения вершин и так же, как были рассмотрены все случаи расположения и . Пусть и -- соответственно кратчайшие простые -цепь и -цепь по внутренней части (рис. 10).
Заметим, что и имеют общую точку.
2.3.1. Пусть цепи и имеют более одной общей точки.
Тогда в графе G есть подграф, гомеоморфный (рис. 11).
2.3.2. Пусть цепи и имеют точно одну общую точку .
Тогда в графе G есть подграф, гомеоморфный (рис. 12).
Таким образом, доказано, что в графе G имеется подграф, гомеоморфный или , что противоречит нашему первому предположению.
Литература
- Асанов М,, Баранский В., Расин В. - Дискретная математика - Графы, матроиды, алгоритмы