Необходимость
Необходимость условия очевидна.
Достаточность
От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных [math] K_{5} [/math] или [math] K_{3, 3} [/math]. Пусть [math] G [/math] - такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин.
G связен
Если [math] G [/math] не связен, то его компоненты связности планарны и, следовательно, сам граф [math] G [/math] планарен.
G - обыкновенный граф
В самом деле, пусть в графе [math] G [/math] есть петля или кратное ребро [math] e [/math]. Тогда граф [math] G - e [/math] планарен. Добавляя ребро [math] e [/math] к графу [math] G - e [/math] получим, что граф [math] G [/math] он планарен.
G - блок
Пусть, от противного, в графе есть точка сочленения [math] v [/math]. Через [math] G_1 [/math] обозначим подграф графа [math] G [/math], порождённый вершинами одной из компонент связности графа [math] G - v[/math] и вершинной [math] v [/math], а через
[math] G_2 [/math] подграф графа [math] G [/math], порождённый вершинами остальных компонент связности графа [math] G - v [/math] и вершиной [math] v [/math]. (рис. 1)
Разбор случаев взаимного положения a, b, c, d, u1, u2, v1, v2
Рассмотрим 2 случая.
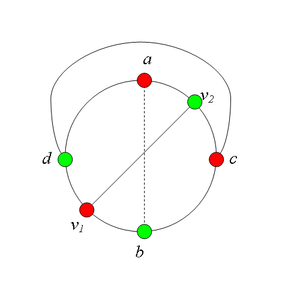
1. Пусть пара вершин [math]\ v_1 [/math] и [math]\ v_2 [/math] является [math](a, b)[/math]-разделяющей.
Тогда, в частности, [math]v_2 \ne a[/math] и [math] v_1 \ne b[/math]. В этом случае граф G содержит подграф, гомеоморфный [math]\ K_{3,3} [/math] (отметим, что в [math] In [/math] существует простая [math](v_1, v_2)[/math]-цепь)(рис. 1).
2. Пусть пара вершин [math]v_1[/math] и [math]v_2[/math] не является [math](a, b)[/math]-разделяющей.
Тогда [math]v_1, v_2[/math] лежат на [math]C[a, b][/math] или на [math]C[b, a][/math]. Без ограничения общности будет считать, что [math]v_1[/math] и [math]v_2[/math] лежат на [math]C[a, b][/math].
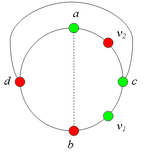
2.1. Пусть [math]v_1[/math] и [math]v_2[/math] лежат на [math]C(a, b)[/math], т.е. [math]v_1 \ne b[/math] и [math]v_2 \ne a[/math](рис. 2).
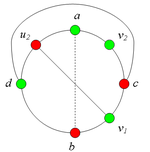
2.1.1 Пусть [math]u_2[/math] лежит на [math]C(d, a)[/math].
Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 3).
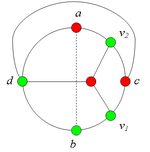
2.1.2. Пусть [math]u_2 = d[/math].
Тогда во внешней части [math]In[/math] имеется вершина [math]w[/math] и три простые цепи от [math]w[/math] соответственно до [math]d, v_1, v_2[/math], которые в качестве общей точки имеют только точку [math]w[/math]. В этом случае в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 4).
2.1.3. Пусть [math]u_2[/math] лежит на [math]C(b, d)[/math].
Тогда в графе G есть подграф, гомеоморфный [math]K{3,3}[/math](рис. 5).
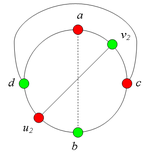
Теперь рассмотрим случаи, когда хотя бы одна из вершин [math]v_1[/math] и [math]v_2[/math] не лежит на [math]С(a, b)[/math]. Без ограничения общности будем считать, что это вершина [math]v_1[/math], т.е [math]v_1 = b[/math](поскольку [math]v_1[/math] лежит на [math]C[a, b][/math]).
2.2. Пусть [math]v_2 \ne a[/math].
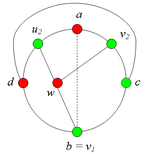
2.2.1. Пусть [math]u_2[/math] лежит на [math]C(d, a)[/math].
Тогда в графе G есть пограф, гомеоморфный [math]K_{3,3}[/math](рис. 6).
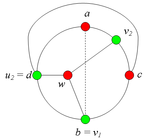
2.2.2. Пусть [math]u_2 = d[/math].
Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 7).
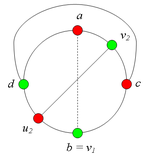
2.2.3. Пусть [math]u_2[/math] лежит на [math]C(b, d)[/math].
Тогда в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math](рис. 8).
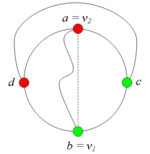
2.3. Пусть [math]v_2 = a[/math](рис. 9).
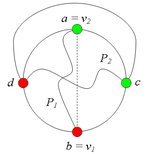
Рассмотрим теперь пару вершин [math]u_1[/math] и [math]u_2[/math]. Будем считать, что [math]u_1 = c[/math] и [math]u_2 = d[/math], поскольку все другие случаи расположения вершин [math]u_1[/math] и [math]u_2[/math] так же, как были рассмотрены все случаи расположения [math]v_1[/math] и [math]v_2[/math]. Пусть [math]P_1[/math] и [math]P_2[/math] -- соответственно кратчайшие простые [math](a, b)[/math]-цепь и [math](c, d)[/math]-цепь по внутренней части [math]In[/math](рис. 10).
Заметим, что [math]P_1[/math] и [math]P_2[/math] имеют общую точку.
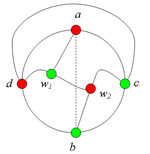
2.3.1. Пусть цепи [math]P_1[/math] и [math]P_2[/math] имеют более одной общей точки.
Тогда в графе G есть подграф, гомеоморфный [math]K_{3,3}[/math](рис. 11).
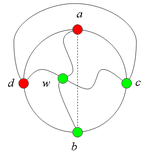
2.3.2. Пусть цепи [math]P_1[/math] и [math]P_2[/math] имеют точно одну общую точку [math]w[/math].
Тогда в графе G есть подграф, гомеоморфный [math]K_5[/math](рис. 12).
Таким образом, доказано, что в графе G имеется подграф, гомеоморфный [math]K_{3,3}[/math] или [math]K_5[/math], что противоречит нашему первому предположению.
|