| Определение: |
| Матрицей Кирхгофа простого графа [math]G = (V,E) [/math] называется матрица [math] K (|V| \times |V|) = \parallel k_{i,j} \parallel [/math], элементы которой определяются равенством: [math]
k_{i,j} =
\begin{cases}
\deg(v_i), \ i = j \\
-1, \ (v_i,v_j) \in E \\
0, \mbox{ otherwise}.
\end{cases}
[/math] |
Иными словами, на главной диагонали матрицы Кирхгофа находятся степени вершин, а на пересечении [math]i[/math]-й строки и [math]j[/math]-го столбца ([math]i \ne j[/math]) стоит [math]-1[/math], если вершины с номерами [math]i[/math] и [math]j[/math] смежны, и [math]0[/math] в противном случае.
Пример матрицы Кирхгофа
| Граф
|
Матрица Кирхгофа
|
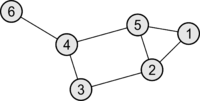
|
[math]\left(\begin{array}{rrrrrr}
2 & -1 & 0 & 0 & -1 & 0\\
-1 & 3 & -1 & 0 & -1 & 0\\
0 & -1 & 2 & -1 & 0 & 0\\
0 & 0 & -1 & 3 & -1 & -1\\
-1 & -1 & 0 & -1 & 3 & 0\\
0 & 0 & 0 & -1 & 0 & 1\\
\end{array}\right)[/math]
|
Некоторые свойства
1. Сумма элементов каждой строки (столбца) матрицы Кирхгофа равна нулю:
- [math]\ \sum_{i=1}^{|V|} k_{i,j} = 0[/math].
2. Определитель матрицы Кирхгофа равен нулю:
- [math]\det K=0[/math]
Доказательство:
[math] \det K =
\begin{vmatrix}
k_{1, 1} & k_{1, 2} & \cdots & k_{1, |V|} \\
k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|}
\end{vmatrix}
[/math]
Прибавим к первой строке все остальные строки(это не изменит значение определителя):
[math]\begin{vmatrix}
k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} \\
k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|}
\end{vmatrix}
[/math]
Так как сумма элементов каждого столбца равна [math]0[/math], получим:
[math]\det K = \begin{vmatrix}
0 & 0 & \cdots & 0 \\
k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|}
\end{vmatrix} = 0
[/math]
3. Матрица Кирхгофа простого графа симметрична:
- [math]\ k_{i,j} = k_{j,i}\quad i,j=1, \ldots, |V|[/math].
4. Связь с матрицей смежности:
- [math] K =
\begin{pmatrix}
\mathrm{deg}(v_1) & 0 & \cdots & 0 \\
0 & \mathrm{deg}(v_2) & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & \mathrm{deg}(v_n)
\end{pmatrix} - A,
[/math]
где [math]A[/math] — матрица смежности графа [math]G[/math].
5. Связь с матрицей инцидентности:
- [math] K = I \cdot I^T, [/math] где [math]I[/math] — матрица инцидентности некоторой ориентации графа.
6. [math]0[/math] является собственным значением матрицы.
Доказательство:
Собственным значением матрицы называют значения [math]\lambda[/math], которые удовлетворяют уравнению:
[math]\begin{vmatrix}
k_{1, 1} - \lambda &k_{1, 2} & \cdots & k_{1, |V|} \\
k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V| - \lambda}
\end{vmatrix} = 0
[/math]
Прибавим к первой строке все остальные строки(это не изменит значение определителя):
[math]\begin{vmatrix}
k_{1, 1} + k_{2, 1} + \cdots + k_{|V|, 1} - \lambda & k_{1, 2} + k_{2, 2} + \cdots + k_{|V|, 2} - \lambda & \cdots & k_{1, |V|} + k_{2, |V|} + \cdots + k_{|V|, |V|} - \lambda \\
k_{2, 1} & k_{2, 2} & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|}
\end{vmatrix}
[/math]
Так как сумма элементов каждого столбца равна [math]0[/math], получим:
[math]\begin{vmatrix}
- \lambda &-\lambda & \cdots & - \lambda \\
k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda
\end{vmatrix} = 0
[/math]
[math]- \lambda
\begin{vmatrix}
1 & 1 & \cdots & 1 \\
k_{2, 1} & k_{2, 2} - \lambda & \cdots & k_{2, |V|} \\
\vdots & \vdots & \ddots & \vdots \\
k_{|V|, 1} & k_{|V|, 2} & \cdots & k_{|V|, |V|} - \lambda
\end{vmatrix}= 0.
[/math]
Следовательно, [math]0[/math] является собственным значением
См. также
Источники информации
