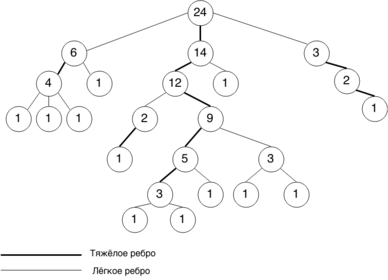
Heavy-light декомпозиция
Heavy-light декомпозиция — техника разбиения подвешенного дерева на множество путей для решения задач о запросах на пути в дереве (в том числе с модификациями).
Содержание
Описание задачи
| Задача: |
| Имеется дерево c вершинами и необходимо проводить операции на нем на пути от вершины до вершины . |
Примеры запросов:
- Сумма на пути
- Максимум на пути
- Количество рёбер на пути, вес которых больше заданного
Примеры модификаций:
- Модификация одного ребра
- Прибавление к весу всех рёбер на пути
- Установка веса всех рёбер на пути в заданное
Множество подобных запросов делаются за время за полином от логарифма (обычно ) с помощью Heavy-light декомпозиции.
Описание декомпозиции
Декомпозиция заключается в классификации всех рёбер дерева в 2 вида: легкие и тяжёлые. Введём функцию , которая будет обозначать размер поддерева вершины .
Тяжёлые ребра (Heavy edge) — ребра такие, что .
Лёгкие ребра (Light edge) — соответственно все остальные.
Очевидно, что из вершины может выходить как максимум одно тяжёлое ребро, т.к. иначе у нас есть два поддерева по как минимум вершин, а также сама вершина . Итого вершин, тогда как у нас всего вершин в поддереве.
Теперь рассмотрим вершины, из которых не ведет вниз ни одно тяжёлое ребро. Будем идти от них вверх до корня или пока не пройдем легкое ребро. Получится какое-то множество путей. Утверждается, что полученная таким путём декомпозиция будет являться искомой и корректной.
| Утверждение: |
Полученная декомпозиция является искомой. |
|
Докажем по отдельности корректность декомпозиции.
|
Существует вариант Heavy-light декомпозиции на вершинно-непересекающихся путях. Чтобы получить такой путь нужно всего-лишь выкинуть последнее ребро из всех путей в рёберно-непересекающейся декомпозиции. Это может быть удобно при решении задач, где веса находятся не на рёбрах, а на вершинах и соответствующие запросы также делаются на вершинах.
Применение
Сумма на пути
Классическая задача о сумме на пути в дереве с решается с помощью Heavy-light декомпозиции за время. Возможны модификации веса.
Построим дерево отрезков над каждым путём. Рассмотрим запрос . Давайте найдем вершину , которая является (например с помощью двоичного подъема. Мы разбили запрос на два: и , на каждый из которых можно легко ответить выбирая путь, содержащий самую нижнюю вершину и вырезать его, пока этот путь не содержит .
Так мы сможем получать ответ на пути за . А всего таких путей нужно будет рассмотреть . Итого мы способны решить эту задачу за время .
Хоть это и не самый эффективный способ для решения этой задачи, но можно заметить, что с помощью такого трюка мы можем решить широкий класс задач просто сведя её к задаче о запросах в дереве отрезков (такие как максимум на пути, покраска на пути, прибавление на пути и др.).
Реализация
Опущены некоторые детали реализации: построение и предподсчёт.
- — функция, позволяющая найти номер пути, относящийся к конкретной вершине.
- — функция, позволяющая найти корень пути (самую верхнюю вершину).
- — функция, позволяющая найти смещение вершины в пути относительно корня пути.
- — функция, позволяющая найти вес -ого ребра в -ом пути.
Пример реализации запроса суммы на пути:
int queryPath(int path, int from, int to):
int res = 0
while from <= to:
if from mod 2 == 1:
res += getValue(path, from)
if to mod 2 == 0:
res += getValue(path, to)
to = (to - 1) / 2
from = (from + 1) / 2
return res
int query(int u, int v):
int res = 0
int root = pathRoot(u)
while not (root is ancestor of v) // поднимаемся до тех пор, пока наш путь не содержит общего предка u и v
res += queryPath(getPath(u), 0, pathPos(u))
u = parent of root // вырезали нижний путь и подняли нижнюю вершину до нижней вершины следующего пути
root = pathRoot(u)
root = pathRoot(v)
while not (root is ancestor of u) // аналогично прошлому while, но с другой стороны
res += queryPath(getPath(v), 0, pathPos(v))
v = parent of root
root = pathRoot(v)
// последний путь (тот, что содержит общего предка) обрезан с двух сторон полученными вершинами
res += queryPath(path(u), min(pathPos(u), pathPos(v)), max(pathPos(u), pathPos(v)))
return res