Теорема Клини (совпадение классов автоматных и регулярных языков)

Теорема (Клини):

Классы автоматных и регулярных языков совпадают.

Доказательство:

[math]\triangleright[/math]

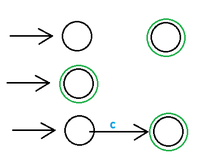
Автоматы для регулярных языков нулевого поколения Автомат для объединения двух регулярных языков Автомат для конкатенации двух регулярных языков Автомат для замыкания Клини регулярного языка 1. [math]\mathrm{REG} \subseteq \mathrm{AUT}[/math]. Для доказательства будем строить автоматы, допускающие регулярные языки (см. картинки справа). При этом будем использовать индукцию по номеру поколения регулярного языка. База. [math]n = 0[/math]. Для этого достаточно построить автоматы для трех языков: [math]L = \varnothing[/math], [math]L = \left\{\varepsilon \right\}[/math], [math]L = \left\{c \right\}[/math]. 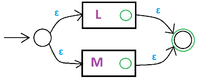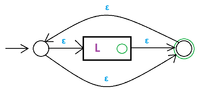Индукционный переход. Умеем строить автоматы для языков [math]n[/math]-ого поколения. Будем строить для [math]n + 1[/math]. Для этого достаточно научиться строить автоматы для следующих языков ([math]L, M \in \mathrm{R_n}[/math]): [math]L^\prime = L \cup M[/math], [math]L^\prime = LM[/math], [math]L^\prime = L^*[/math]. Заметим, что по предположению индукции автоматы для [math]L, M[/math] могут быть построены. Итого, мы можем по регулярному выражению построить автомат, допускающий тот же язык. 2. [math]\mathrm{AUT} \subseteq \mathrm{REG}[/math]. Для доказательства будем строить регулярное выражение, допускающее язык, заданный каким-то автоматом. Пусть задан автомат [math]A[/math] с набором состояний [math]Q = \left\{1, 2, \dots n \right\}[/math]. Определим регулярные выражения, задающие следующие множества слов: [math]\xi_{ijk} = \left\{ s \mid \langle i,s \rangle \vdash^* \langle j, \varepsilon \rangle \right\} [/math], причем в качестве промежуточных вершин выступают только такие, у которых номер не более [math]k[/math]. Построим эти регулярные выражения: [math]\xi_{ii0} = (c_1 \mid \dots \mid c_l)^*[/math] , где [math]c_1, c_2, \dots c_l[/math] символы, по которым есть переход из состояния [math]i[/math] в него же самого. [math]\xi_{ij0} = c_1 \mid \dots \mid c_l[/math], где [math]c_1, c_2, \dots c_l[/math] символы, по которым есть переход из состояния [math]i[/math] в состояние [math]j[/math]. [math]\xi_{iik} = (\xi_{ii{k-1}} \mid \xi_{ik{k-1}} (\xi_{kk{k-1}})^* \xi_{ki{k-1}} )^*[/math]. [math]\xi_{ijk} = \xi_{ij{k-1}} \mid \xi_{ik{k-1}} (\xi_{kk{k-1}})^* \xi_{kj{k-1}}[/math]. Теперь нетрудно задать регулярное выражение для всего языка: [math]\varphi = \xi_{s{t_1}n} \mid \xi_{s{t_2}n} \mid \dots \mid \xi_{s{t_r}n}[/math], где [math]s[/math] — стартовое состояние, а [math]t_1, t_2, \dots t_r[/math] — терминальные состояния исходного автомата. Таким образом, мы построили по автомату регулярное выражение, допускающее тот же самый язык.

[math]\triangleleft[/math]