Алгоритм Хаффмана

Определение

Определение:

Коды или Алгоритм Хаффмана (Huffman codes) — широко распространенный и очень эффективный метод сжатия данных, который, в зависимости от характеристик этих данных, обычно позволяет сэкономить от 20% до 90% объема.

Рассматриваются данные, представляющие собой последовательность символов. В жадном алгоритме Хаффмана используется таблица, содержащая частоты появления тех или иных символов. С помощью этой таблицы определяется оптимальное представление каждого символа в виде бинарной строки.

Построение кода Хаффмана

В основу алгоритма Хаффмана положена идея: кодировать более коротко те символы, которые встречаются чаще, а те, которые встречаются реже кодировать длиннее. Для построения кода Хаффмана нам необходима таблица частот символов. Рассмотрим пример построения кода на простой строке abacaba

a	b	c
4	2	1

Следующим шагом будет построение дерева, где вершины - "символы", а пути до них соответствуют их префиксным кодам. Для этого на каждом шаге будем брать два символа с минимальной частотой вхождения, и объединять их в новые так называемые "символы" с частотой равной сумме частот тех символов, которые мы объединяли. В примере мы объединим символы b и с в символ bc с частотой 3. Файл:Haffman1.jpg

Хаффман изобрел жадный алгоритм, позволяющий составить оптимальный префиксный код, который получил название код Хаффмана. Доказательство корректности этого алгоритма основывается на свойстве жадного выбора и оптимальной подструктуре. Вместо того чтобы демонстрировать, что эти свойства выполняются, а затем разрабатывать псевдокод, сначала мы представим псевдокод. Это поможет прояснить, как алгоритм осуществляет жадный выбор. В приведенном ниже псевдокоде предполагается, что [math]C[/math] — множество, состоящее из [math]n[/math] символов, и что каждый из символов [math]c\in C[/math] — объект с определенной частотой [math]f(c)[/math]. В алгоритме строится дерево [math]T[/math], соответствующее оптимальному коду, причем построение идет в восходящем направлении. Процесс построения начинается с множества, состоящего из [math]|C|[/math] листьев, после чего последовательно выполняется [math]|C|-1[/math] операций "слияния", в результате которых образуется конечное дерево. Для идентификации двух наименее часто встречающихся объектов, подлежащих слиянию, используется очередь с приоритетами [math]Q[/math], ключами в которой являются частоты [math]f[/math]. В результате слияния двух объектов образуется новый объект, частота появления которого является суммой частот объединенных объектов:

Huffman([math]C[/math])
[math]n \gets |C|[/math]
[math]Q \gets C[/math]
for [math]i \gets 1[/math] to [math]n - 1[/math]

do Выделить память для узла [math]z[/math]

left[[math] z[/math]][math] \gets x \gets[/math] Extract_Min([math] Q[/math])

right[[math]z[/math]][math]\gets y \gets [/math] Extract_Min([math]Q[/math])

[math]f[z] \gets f[x]+f[y][/math]

Insert([math]Q[/math], [math]z[/math] )

return Extract_Min([math]Q[/math] ) [math] \rhd [/math] Возврат корня дерева

Пример работы алгоритма

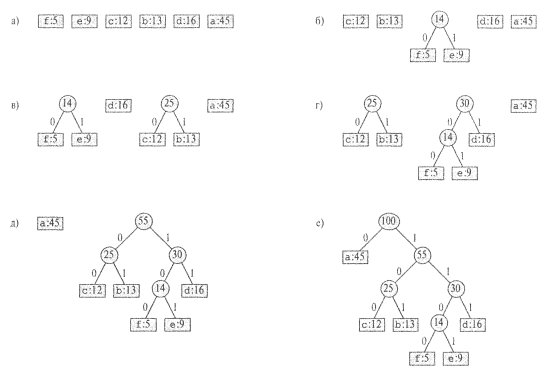
На каждом этапе показано содержимое очереди, элементы которой рассортированы в порядке возрастания их частот. На каждом шаге работы алгоритма объединяются два объекта (дерева) с самыми низкими частотами. Листья изображены в виде прямоугольников, в каждом из которых указана буква и соответствующая ей частота. Внутренние узлы представлены кругами, содержащими сумму частот дочерних узлов. Ребро, соединяющее внутренний узел с левым дочерним узлом, имеет метку 0, а ребро, соединяющее его с правым дочерним узлом, — метку 1. Слово кода для буквы образуется последовательностью меток на ребрах, соединяющих корень с листом, представляющим эту букву. По скольку данное множество содержит шесть букв, размер исходной очереди равен 6(часть а рисунка), а для построения дерева требуется пять слияний. Промежуточные этапы изображены в частях б-д. Конечное дерево (е) представляет оптимальный префиксный код. Как уже говорилось, слово кода для буквы — это последовательность меток на пути от корня к листу с этой буквой.
В строке 2 инициализируется очередь с приоритетами [math]Q[/math], состоящая из элементов множества [math]С[/math]. Цикл for в строках 3-8 поочередно извлекает по два узла, [math]x[/math] и [math]у[/math], которые характеризуются в очереди наименьшими частотами, и заменяет их в очереди новым узлом, представляющим объединение упомянутых выше элементов. Частота появления [math]z[/math] вычисляется в строке 7 как сумма частот [math]x[/math] и [math]y[/math]. Узел [math]x[/math] является левым дочерним узлом [math]z[/math], а [math]y[/math] — его правым дочерним узлом. (Этот порядок является произвольным; перестановка левого и правого дочерних узлов приводит к созданию другого кода с той же стоимостью.) После [math]n - 1[/math] объединений в очереди остается один узел — корень дерева кодов, который возвращается в строке 9.

Оценка времени работы

При анализе времени работы алгоритма Хаффмана предполагается, что [math]Q[/math] реализована как бинарная неубывающая пирамида. Для множества [math]C[/math], состоящего из [math]n[/math] символов, инициализацию очереди [math]Q[/math] в строке 2 можно выполнить за время [math]O(n)[/math]. Цикл for в строках 3-8 выполняется ровно [math]n - 1[/math] раз, и поскольку для каждой операции над пирамидой требуется время[math]O(lg(n))[/math], вклад цикла во время работы алгоритма равен [math]O(n \cdot lg(n))[/math]. Таким образом, полное время работы процедуры Huffman с входным множеством, состоящим из [math]n[/math] символов, равно [math]O(n \cdot lg(n))[/math].

Корректность алгоритма Хаффмана

Чтобы доказать корректность жадного алгоритма Huffman, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Лемма (1):

Пусть [math]C[/math] — алфавит, каждый символ [math]c \in C[/math] которого встречается с частотой [math]f[c][/math]. Пусть [math]x[/math] и [math]y[/math] — два символа алфавита [math]C[/math] с самыми низкими частотами. Тогда для алфавита [math]C[/math] существует оптимальный префиксный код, кодовые слова символов [math]x[/math] и [math]y[/math] в котором имеют одинаковую длину и отличаются лишь последним битом.

Доказательство:

[math]\triangleright[/math]

Идея доказательства состоит в том, чтобы взять дерево [math]T[/math], представляющее произвольный оптимальный префиксный код, и преобразовать его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] являются листьями с общим родительским узлом, причем в новом дереве эти листья находятся на максимальной глубине. Пусть [math]a[/math] и [math]b[/math] — два символа, представленные листьями с общим родительским узлом, которые находятся на максимальной глубине дерева [math]T[/math]. Предположим без потери общности, что [math]f[a] \le f[b][/math] и [math]f[x] \le f[y][/math]. Поскольку [math]f[x][/math] и [math]f[y][/math] — две самые маленькие частоты (в указанном порядке), [math]f[a][/math] и [math]f[b][/math] — две произвольные частоты, то выполняются соотношения [math]f[x] \le f[a][/math] и [math]f[y] \le f[b][/math]. В результате перестановки в дереве [math]T[/math] листьев [math]a[/math] и [math]x[/math] получается дерево [math]T'[/math], а при последующей перестановке в дереве V листьев [math]b[/math] и [math]y[/math] получается дерево [math]T''[/math]. Разность стоимостей деревьев Т и Т" равна [math]B(T) - B(T') = \sum_{c \in C} f(c)d_T(C) - \sum_{c \in C} f(c)d_{T'}(C) =[/math] [math] = (f[a] - f[x])(d_T(a) - d_T(x)) \ge 0[/math], поскольку величины [math]f[a] - f[x][/math] и [math]d_T(a) - d_T(x)[/math] неотрицательны. Величина [math]f[a] - f[x][/math] неотрицательна, потому что х — лист с минимальной частотой, величина [math]d_T(a) - d_T(x)[/math] неотрицательна, потому что [math]a[/math] — лист на максимальной глубине в дереве [math]T[/math]. Аналогично, перестановка листьев [math]y[/math] и [math]b[/math] не приведет к увеличению стоимости, поэтому величина [math]B(T') - B(T'')[/math] неотрицательна. Таким образом, выполняется неравенство [math]B(T') \le B(T'')[/math], и поскольку [math]T[/math] — оптимальное дерево, то должно также выполняться неравенство [math]B(T'') \le B(T')[/math], откуда следует, что [math]B(T') = B(T'')[/math]. Таким образом, [math]T''[/math] — оптимальное дерево, в котором [math]x[/math] и [math]y[/math] — находящиеся на максимальной глубине дочерние листья одного и того же узла, что и доказывает лемму.

[math]\triangleleft[/math]

Лемма (2):

Пусть дан алфавит [math]C[/math], в котором для каждого символа [math]c \in C[/math] определены частоты [math]f[c][/math]. Пусть [math]x[/math] и [math]y[/math] — два символа из алфавита [math]C[/math] с минимальными частотами. Пусть [math]C'[/math] — алфавит, полученный из алфавита [math]C[/math] путем удаления символов [math]x[/math] и [math]y[/math] и добавления нового символа [math]z[/math], так что [math]C = C — {х,у} \cup {z}[/math]. По определению частоты [math]f[/math] в алфавите [math]C'[/math] совпадают с частотами в алфавите [math]C[/math], за исключением частоты [math]f[z] = f[x] + f[y][/math]. Пусть [math]T'[/math] — произвольное дерево, представляющее оптимальный префиксный код для алфавита [math]C'[/math] Тогда дерево [math]T[/math], полученное из дерева [math]T'[/math] путем замены листа [math]z[/math] внутренним узлом с дочерними элементами [math]x[/math] и [math]y[/math], представляет оптимальный префиксный код для алфавита [math]C[/math].

Доказательство:

[math]\triangleright[/math]

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] можно выразить через стоимость [math]B(T')[/math] дерева [math]T'[/math]. Для каждого символа [math]c \le C - {x,y}[/math] выполняется соотношение [math]d_T(C) = d_{T'}(c)[/math], следовательно, [math]f[c]d_T(C) = f[c]d_{T'}(c)[/math]. Поскольку [math]d_T(x) = d_{T}(y) = d_{t'}(z) + 1[/math], получаем соотношение [math]f[x]d_T(x) + f[y]d_{T}(y) = (f[x] + f[y])(d_{T'}(z) + 1) = f[z]d_{T'}(z) + (f[x] + f[y])[/math] из которого следует равенство [math] B(T) = B(T') + f[x] + f[y] [/math] ИЛИ [math] B(T') = B(T) - f[x] - f[y] [/math]. Докажем лемму методом от противного. Предположим, дерево [math] T [/math] не представляет оптимальный префиксный код для алфавита [math] C [/math]. Тогда существует дерево [math] T'' [/math], для которого справедливо неравенство [math] B(T'') \lt B(T) [/math]. Согласно лемме (1), [math]x[/math] и [math]y[/math] без потери общности можно считать дочерними элементами одного и того же узла. Пусть дерево [math]T'''[/math] получено из дерева [math]T''[/math] путем замены элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y] [/math]. Тогда можно записать: [math]B(T''') = B(T'') - f[x] - f[y] \lt B(T) - f[x] -f[y] = B(T')[/math], что противоречит предположению о том, что дерево [math]T'[/math] представляет оптимальный префиксный код для алфавита [math]C'[/math]. Таким образом, дерево [math]T[/math] должно представлять оптимальный префиксный код для алфавита [math]C[/math].

[math]\triangleleft[/math]

Лемма 16.3. Доказательство.

Теорема:

Процедура Huffman дает оптимальный префиксный код.

Доказательство:

[math]\triangleright[/math]

Справедливость теоремы непосредственно следует из лемм (1) и (2)

[math]\triangleleft[/math]

Литература

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — С. 1296. — ISBN 5-8489-0857-4