Хроматическое число планарного графа
Для планарного графа можно дать оценку сверху на хроматическое число.
Раскраска в 6 цветов
| Лемма: |
В любом графе существует вершина степени не больше . |
| Доказательство: |
| Предположим это не так. Для любой вершины графа верно . Если сложить это неравенство для всех , получим . Но по следствию из теоремы Эйлера . Пришли к противоречию. |
| Теорема: |
Пусть граф — планарный. Тогда |
| Доказательство: |
|
Докажем по индукции. База индукции Если граф содержит не более вершин, то очевидно, что Индукционный переход Предположим, что для планарного графа с вершинами существует раскраска в цветов. Докажем то же для графа с вершиной. По только что доказанной лемме в найдётся вершина степени не больше . Удалим её; по предположению индукции получившийся граф можно раскрасить в цветов. Вернём удалённую вершину и покрасим её в цвет, не встречающийся среди смежных ей вершин (ведь "занято" максимум цветов). Индукционный переход доказан. |
Раскраска в 5 цветов
| Теорема (Хивуд): |
Пусть граф — планарный. Тогда |
| Доказательство: |
|
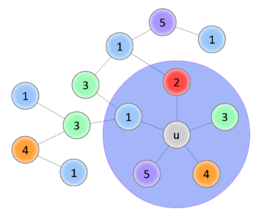
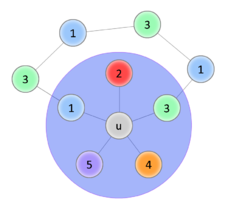
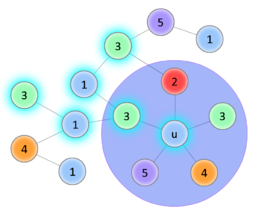
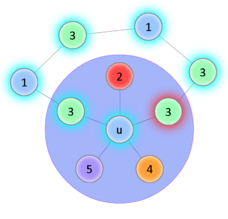
Начало доказательства такое же, как в предыдущей теореме, трудность возникает в индукционном переходе. Покажем что для случая с -ю цветами всё равно можно вернуть удалённую вершину так, чтобы раскраска осталась правильной. Обозначим за — возвращаемую вершину, — вершину, покрашенную в цвет. Если среди вершин, смежных , есть две вершины одного цвета, значит остаётся по меньшей мере один свободный цвет, в который мы и покрасим . Иначе, уложим полученный после удаления граф на плоскость, вернём вершину (пока бесцветную) и пронумеруем цвета в порядке обхода смежных вершин по часовой стрелке. Попробуем покрасить в цвет . Чтобы раскраска осталась правильной, перекрасим смежную ей вершину в цвет . Если среди смежных ей вершин есть вершины , покрасим их в цвет , и так далее. Рассмотрим две необычные ситуации, которые могут наступить во время обхода:
Если этот процесс был успешно завершён, то получили правильную раскраску. Если же в соответствии со вторым вариантом перекраска не удалась, это означает, что в графе есть цикл . Тогда попытаемся таким же образом перекрасить в цвет , а смежную ей в цвет (со последующими перекрасками). Если удастся — раскраска получена. Если нет, то получили ещё один цикл . Но граф планарный, значит два полученных цикла пересекаются помимо вершины по крайней мере ещё в одной, что невозможно, ведь вершины первого цикла и второго — разных цветов. Значит такой случай наступить не мог. |
| Успешное перекрашивание | Цикл 1—3, перекрасить не удаётся | ||||||||||
 |
| ||||||||||
 |
|
Заметим, что не удаётся составить подобное доказательство для раскраски в четыре цвета, поскольку здесь наличие двух вершин одного цвета среди смежных не исключает того, что при их (смежных вершин) раскраске использовались все возможные цвета.
Раскраска в 4 цвета
Данная теорема была доказана Кеннетом Аппелем и Вольфгангом Хакеном. Их доказательство сводилось к рассмотрению порядка 2000 графов, 4-раскрашиваемость которых была проверена при помощи компьютера[1].