|
Докажем для начала ряд вспомогательных лемм.
| Лемма (I): |
Граф [math]G[/math] планарен тогда и только тогда, когда он обладает укладкой на сфере |
| Доказательство: |
| [math]\triangleright[/math] | |
Рассмотрим укладку графа [math]G[/math] на сфере. Возьмем на сфере точку [math]N[/math], не лежащую на ребре, и не вершину. Выберем на сфере точку [math]S[/math] противолежащую [math]N[/math] ([math]N[/math] и [math]S[/math] лежат на одном диаметре и при этом не совпадают). Проведем через точку [math]S[/math] касательную к сфере плоскость. Спроектируем на плоскость все точки сферы, проведя все возможные лучи из точки [math]N[/math] через точки сферы до пересечения с плоскостью (рис. 1) . Ясно, что эта проекция дает укладку графа [math]G[/math] на плоскости.
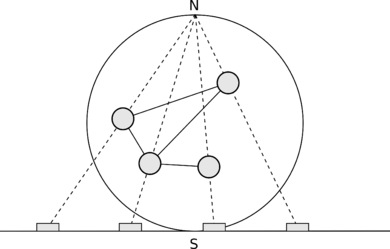 рис. 1. Проекция графа со сферы на плоскость. [math]S[/math] — точка касания, [math]N[/math] — противоположная точка.
Обратно рассмотрим укладку графа [math]G[/math] на плоскости. Возьмем сферу, которая касается плоскости, и обозначим точку касания за [math]S[/math]. Противолежащую [math]S[/math] точку на сфере обозначим за [math]N[/math]. Проведем все возможные лучи от точек плоскости через точки сферы до точки [math]N[/math]. Ясно что при этом укладка графа [math]G[/math] на плоскости будет перенесена на некоторую укладку графа [math]G[/math] на сфере. | | [math]\triangleleft[/math] |
| Лемма (II): |
Для любого выделенного ребра планарного графа найдется такая укладка графа на плоскости, что выделенное ребро будет лежать на границе внешней грани. |
| Доказательство: |
| [math]\triangleright[/math] | |
Возьмем укладку графа на сфере. Перенесем эту укладку графа на сфере в укладку на плоскости так как это сделано в лемме I, за точку [math]N[/math] возьмем точку на сфере, не лежащую на ребре, не являющуюся вершиной и принадлежащую грани на границе которой лежит выделенное ребро. Полученная укладка на плоскости обладает нужным нам свойством (рис. 2).
| | [math]\triangleleft[/math] |
Докажем утверждение теоремы для одной из компонент связности графа [math]G[/math]. Ясно, что имея укладки на плоскости каждой из компонент связности графа, мы можем получить укладку на плоскости и всего графа.
Итак пусть граф [math]G[/math] связен. Рассмотрим связный подграф [math]T[/math] графа компонент реберной двусвязности графа [math]G[/math]. Из леммы и из связности [math]T[/math] получаем, что [math]T[/math] — дерево.
Докажем индукцией по числу вершин в графе [math]T[/math], что подграф [math]G'[/math] графа [math]G[/math] состоящий из компонент реберной двусвязности и мостов графа [math]G[/math] принадлежащих графу [math]T[/math] планарен (далее будем говорить, что [math]G'[/math] соответствует [math]T[/math]).
База индукции.
Если [math]|VT| = 1[/math], то граф [math]T[/math] — тривиальный граф. Его единственная вершина - это компонента реберной двусвязности графа [math]G[/math], которая по условию теоремы планарна.
Индукционный переход.
Пусть утверждение верно для [math]|VT| \lt m[/math]. Рассмотрим [math]T[/math], для которого [math]|VT| = m \gt 1[/math], и соответствующий [math]T[/math] подграф [math]G'[/math] графа [math]G[/math]. Докажем, что [math]G'[/math] планарен.
Положим [math]G_1[/math] — компонента реберной двусвязности графа [math]G'[/math] являющийся висячей вершиной дерева [math]T[/math], a [math]e[/math] — мост в [math]G'[/math] инцидентный [math]G_1[/math] в [math]T[/math] (рис. 3). [math]G_1[/math] планарен по условию теоремы, т.к. компоненты реберной двусвязности графа [math]G'[/math] совпадают с компонентами реберной двусвязности графа [math]G[/math]. Далее рассмотрим подграф [math]G_2[/math] графа [math]G'[/math], соответствующий дереву [math]T\backslash \{G_1\}[/math]. Поскольку [math]G_1[/math] — висячая вершина [math]T[/math], то [math]T\backslash \{G_1\}[/math] связен, и, очевидно, также как и [math]T[/math] является подграфом графа компонент реберной двусвязности [math]G[/math]. Итак [math]G_2[/math] планарен по предположению индукции, т.к. [math]|V(T\backslash \{G_1\})| = |VT| - 1 = m - 1 \lt m[/math].
Из определения ребер графа компонент реберной двусвязности получаем, что графы [math]G_1[/math] и [math]G_2[/math] соединены в графе [math]G'[/math] единственным мостом [math]e \in G'[/math] инцидентным блоку [math]G_1[/math] в дереве [math]T[/math]. Поскольку [math]T = G_1\cup e\cup G_2[/math], то и [math]G' = G_1\cup e\cup G_2[/math]. Покажем как из укладок [math]G_1[/math] и [math]G_2[/math] получить укладку [math]G'[/math].
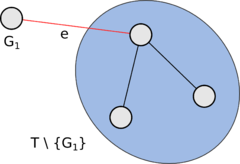 рис. 3. Удаление [math]G_1[/math] из графа компонент реберной двусвязности Уложим [math]G_2[/math] на сфере и уложим [math]G_1[/math] на плоскости так, чтобы ребро [math]e_1 \in G_1[/math] смежное с [math]e[/math] в G' (если таковое имеется) оказалось на границе внешней грани (по лемме II это возможно, рис. 4). Если такого ребра [math]e_1[/math] не существует, значит компонента реберной двусвязности [math]G_1[/math] — тривиальный граф, в таком случае возьмем любую укладку [math]G_1[/math] на плоскости. Пусть [math]u\in G_2[/math] — вершина инцидентная [math]e[/math]. Сожмем часть плоскости, содержащую укладку [math]G_1[/math], так, чтобы она вмещалась в одну из граней укладки [math]G_2[/math] смежную с [math]u[/math]. Проведем жорднанову кривую, соответствующую ребру [math]e[/math], от вершины [math]u[/math] к инцидентной [math]e[/math] вершине графа [math]G_1[/math] так, чтобы она не пересекалась с укладками [math]G_1[/math] и [math]G_2[/math]. Мы получили укладку графа [math]G'[/math] на сфере, а значит (по лемме I) [math]G'[/math] планарен, следовательно предположение индукции верно.
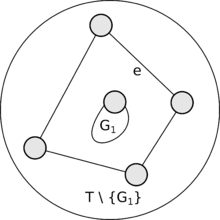 рис. 4. Укладка [math]G_1[/math] и [math]G_2[/math] на сфере
Рассматривая в качестве [math]T[/math] граф компонент реберной двусвязности [math]G[/math] получаем что [math]G[/math] - планарен. |