Гиперграфы
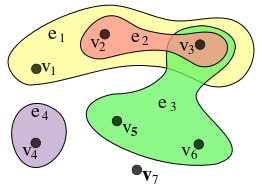
Гиперграфом (англ. hypergraph) называется обобщение графа, в котором каждое ребро соединяет необязательно две вершины. Формально, гиперграф — упорядоченная пара , где — множество вершин гиперграфа, а — множество ребер гиперграфа, где каждое ребро является подмножеством множества вершин.
В дальнейшем будем считать, что все рассматриваемые гипергафы обладают свойствами:
Стоит заметить, что обычный граф является частным случаем гиперграфа, где каждое ребро имеет мощность .
Определения
Подгиперграфом (англ. subhypergraph) гиперграфа назывется гипергаф: . Иначе, подгипергаф — это гипергаф с некоторомы удаленными вершинами.
Реберным гиперграфом (англ. dual) называется гипергаф: , где вершина принадлежит ребру , если вершина принадлежит ребру в исходном гиперграфе . Оче
Свойства
Ацикличность
Заметим, что гиперграф удобно задавать матрицей инцидентности.