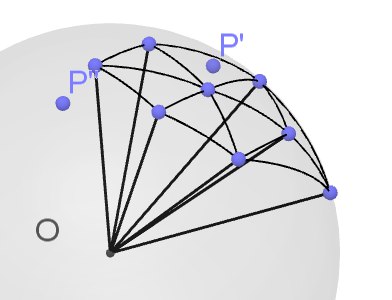
Триангуляция Делоне на сфере

Определения

Определение:

Триангуляция — набор непересекающихся отрезков, соединяющий заданный набор точек так, что добавление новых отрезков невозможно без пересечения уже имеющихся.

Определение:

Критерий Делоне (частный случай для сферы): при построении плоскости через три точки, которые образуют треугольник, все остальные точки лежат не выше этой плоскости.

Существование триангуляции Делоне

Лемма (1):

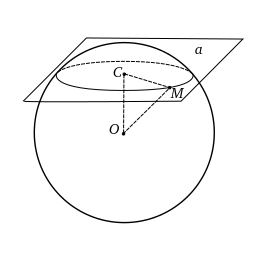
Сечение сферы плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к пересекаемой плоскости, есть центр круга, полученного в сечении.

Доказательство:

[math]\triangleright[/math]

Пусть плоскость [math]\alpha[/math] пересекает сферу. Из центра [math]O[/math] опустим перпендикуляр [math]OC[/math] на плоскость [math]\alpha[/math]. Соединим произвольную точку [math]M[/math] линии пересечения плоскости [math]\alpha[/math] со сферой с точками [math]O[/math] и [math]C[/math]. Так как [math]OC[/math] ⊥ [math]\alpha[/math], то [math]OC[/math] ⊥ [math]CM[/math]. Рассмотрим треугольник △[math] OCM [/math] : [math] CM^2 = OM^2 - OC^2[/math]. Т.к. [math]OM[/math] и [math]OC[/math] - величины постоянные, то и [math]CM[/math] - величина постоянная. Таким образом все точки линии пересечения плоскости [math]\alpha[/math] и сферы равноудалены от точки [math]C[/math], поэтому эта линия пересечения является окружностью с центром в точке [math]C[/math] и радиусом [math]r = CM[/math].

[math]\triangleleft[/math]

Теорема:

Триангуляция Делоне существует, причём для каждого набора точек, в котором никакие четыре точки не лежат на одной окружности, она единственна.

Доказательство:

[math]\triangleright[/math]

Построим выпуклую оболочку наших точек. Все грани выпуклой оболочки окажутся внутри сферы. Поскольку, все точки лежат на сфере, не найдётся точек, которые будут лежать за гранями выпуклой оболочки, иначе выпуклую оболочку можно было бы расширить. Таким образом, все точки, будут принадлежать выпуклой оболочке. Так же ясно,что критерий Делоне будет выполняться, поскольку для каждой грани не будет точек, которые лежат выше нее. Поскольку никакие четыре точки не лежат на одной окружности в исходном наборе точек, а значит, гранями выпуклой оболочки будут треугольнички. Значит, триангуляция существует. А поскольку выпуклая оболочка единственна, можно сказать, что и триангуляция единственна.

[math]\triangleleft[/math]

Лемма (2):

Гранями выпуклой оболочки будут выпуклые многоугольники

Доказательство:

[math]\triangleright[/math]

По определению, множество является выпуклым, если для любых двух точек, отрезок, соединяющий эти точки, тоже входит во множество. И наша оболочка является выпуклой. Предположим, что грань выпуклой оболочки не выпуклый многоугольник. Тогда найдутся две точки, такие, что отрезок не лежит в грани. Тогда получается, что и вся оболочка не является выпуклой.

[math]\triangleleft[/math]

Лемма (3):

Если гранью выпуклой оболочки оказался многоугольник, то любая триангуляция данного многоугольника - триангуляция Делоне.

Доказательство:

[math]\triangleright[/math]

Рассмотрим наш многоугольник и плоскость, построенную через любые три точки. Если существует точка выше нашей плоскости, то мы могли бы расширить нашу выпуклую оболочку, что означает некорректность построенной выпуклой оболочки. Противоречие. Если существует точка ниже нашей плоскости, то "внутри" выпуклой оболочки содержится точка, что некорректно. Противоречие. Отсюда, все точки лежат на плоскости, что в нашем случае эквивалентно тому, что они лежат на одной окружности, значит любая триангуляция нашего многоугольника не нарушит глобальный критерий Делоне(ни в одной окружности, построенной на появившихся в ходе триангуляции треугольников, не будет содержаться точек).

[math]\triangleleft[/math]

Воспользовавшись фактом выше, приходим к очевидному решению как за [math]O(K)[/math] (где [math] K [/math]- количество вершин в многоугольнике) триангулировать все многограники: берем любую точку в многогранике и соединяем её с остальными. Так как в конечной триангуляции мы имеем [math]O(N)[/math] треугольников, а каждый шаг мы добавляем 1 треугольник, то суммарно для всех многоугольник мы совершим не более [math]O(N)[/math] операций.

Статический алгоритм

Алгоритм

Дополним множество наших точек, точкой [math]O[/math], являющейся центром сферы. Данная точка нам понадобится, если все точки оказались в одной полусфере.(более быстрая проверка, на то какие треугольники надо исключить, чем подсчет предиката).

1. Построим для данного множества выпуклую оболочку
2. Удалим все треугольники, которые содеражат вершину [math]O[/math] (это обязательно будут треугольники и они будут существовать только в том случае, если точки лежат в одной полусфере)
3. Пройдемся по всем "выжившим" граням выпуклой оболочки и триангулируем их.

Корректность

Корректность следует из теорем выше.

Время работы

Мы можем построить выпуклую оболочку за [math] \mathcal{O}(N \log(N)) [/math], где [math]N[/math] — количество точек. Удалить треугольники мы можем за [math]O(N)[/math]. Триангулиравать грани мы можем за [math]O(N)[/math] как было показано выше.

В результате получаем [math] \mathcal{O}(N \log(N)) [/math],

Локальный критерий Делоне

Определение:

Локальный критерий Делоне: при построении плоскости через три точки, образующие треугольник, противолежащие сторонам треугольника вершины соседей лежат ниже этой плоскости.

Утверждение:

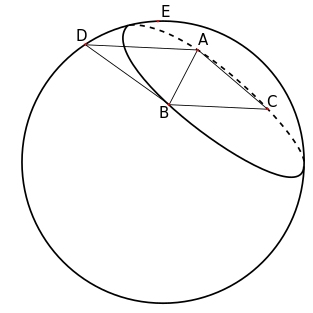
Пусть имеются два треугольника на сфере: [math]ABC[/math] и [math]ABD[/math] и точка [math]E[/math], находящаяся над плоскостью [math]ABC[/math]. Точка [math]D[/math] находится ниже плоскости [math]ABC[/math]. Сечение построенной на ребре [math]AB[/math] и точке [math]O[/math] делит сферу на две полусферы. Если полусфера, не содержащяя треугольник [math]ABC[/math], содержит точки [math]E[/math] и [math]D[/math], то точка [math]E[/math] лежит надо плоскостью [math]ABD[/math].

[math]\triangleright[/math]

Факт очевиден.

[math]\triangleleft[/math]

Утверждение:

Глобальный и локальный критерии Делоне равносильны.

[math]\triangleright[/math]

Из глобального в локальный очевидно. Из локального в глобальный: Пусть выполняется локальный критерий, то есть для каждого треугольника мы можем провести плоскость, что соседние вершины для треугольника будут лежать не выше нашей плоскости. Но нашелся треугольник [math]ABC[/math], что для него не выполняется глобальный критерий, т.е существует какая-то точка [math]E[/math], которая лежит выше плоскости [math]ABC[/math]. В силу того, что локальный критерий выполняется, эта точка не принадлежит соседним треугольникам, в частности смежному треугольнику [math]ABD[/math] по ребру [math]AB[/math] За [math]AB[/math] мы обозначили ребро, из которого видна точка [math]E[/math], т.е такое ребро, что если провести сечение через точки [math]A[/math], [math]B[/math] и [math]O[/math] (центр окружности), то точка [math]E[/math] содержится в полусфере, не содержащей треугольник [math]ABC[/math]. Так как точка [math]E[/math] лежит над плоскостью [math]ABC[/math], а точка [math]D[/math] под плоскостью [math]ABC[/math], то точка [math]E[/math] лежит над плоскостью [math]ABD[/math].(с учетом того, что они лежат в одной полусфере, ребро AB общее и отделяет треугольник [math]ABC[/math] от полусферы) (по утверждению выше) Посмотрим, существует ли у треугольника [math]ABD[/math] смежный треугольник, содержащий вершину [math]E[/math]: Если он существует, то локальный критерий для треугольника [math]ADE[/math] не выполняется. Противоречие. Если он не существует, то точка [math]E[/math] так же будет лежать "над" каким-то смежным с [math]ABD[/math] треугольником, так как для треугольника [math]ABD[/math] будут выполняться те же условия, что и для [math]ABC[/math]. Перейдем к такому треугольнику и повторим шаг. Заметим, что наш процесс есть локализация. Мы пустили луч (в ту сторону, где видим точку [math]E[/math]) из исходного треугольника и идём вдоль него. В какой-то момент мы окажемся рядом с треугольником [math]XYZ[/math], для которого точка E выше плоскости, построенной на его трех точках, и в тоже время вершина E содержится в соседнем треугольнике, что нарушает локальный критерий. Противоречие. Значит глобальный критерий Делоне выполняется.

[math]\triangleleft[/math]

Критерии Делоне для ребер

Определение:

Глобальный критерий Делоне для ребра: через ребро можно провести плоскость так, что все точки будут лежать не выше этой плоскости.

Определение:

Локальный критерий Делоне для ребра: через ребро можно провести плоскость так, что вершины, противолежащие этому ребру, будут лежать не выше этой плоскости

Утверждение:

Глобальный и локальный критерии Делоне для ребра равносильны.

[math]\triangleright[/math]

Из глобального в локальный очевидно, докажем обратно. Предположим противное, то есть найдётся такая плоскость, что вершины треугольников при ребре [math]AB[/math] лежат под ней, но существует какая-то вершина [math]F[/math] над ней. Проведём окружность с центром в сфере через [math]AB[/math] и выберем треугольник лежащий в одной полусфере с точкой [math]F[/math], назовём его [math]ABC[/math]. Точка [math]F[/math] лежит над плоскостью [math]ABC[/math] [math]\implies[/math] [math]F[/math] лежит внутри окружности около [math]ABC[/math]. Возьмем треугольника при ребре, в чьем сегменте оказалась точка [math]F[/math] и назовем его [math]ABC[/math]. Если не существует смежный с ним треугольник при вершине [math]F[/math], то повторим итерацию, иначе противоречие с локальным критерием Делоне.

[math]\triangleleft[/math]

Утверждение:

Критерии Делоне для ребер и треугольников равносильны.

[math]\triangleright[/math]

Из треугольника в ребра: если для каждого треугольника выполнен критерий, то для каждого ребра можно рассматривать плоскость при любом треугольнике при ребре. Обратно: Рассмотрим треугольник [math]ABC[/math], для каждого из ребра можно провести плоскость, такую что все точки будут лежать не выше её. Три плоскости образуют трехмерный угол, снаружи которого нет точек (снаружи == выше каждой плоскости при ребре). В пересечении угла и плосокости [math]ABC[/math] образуется тетраэдр. Если в нем нет точек, значит точек нету и над плоскостью треугольника (точек снаружи тетраэдра нету), значит глобальный критерий выполняется. Проверим это. Пусть в нем есть точки, тогда эти точки оказались внутри треугольника, тогда это не триангуляция.

[math]\triangleleft[/math]

Будем называть хорошими те рёбра, для которых выполняется локальный критерий Делоне.

Лемма (4):

Из двух рёбер, которые можно провести для пары треугольников, как минимум одно хорошее.

Динамический алгоритм

Определение:

Рассмотрим пару смежных треугольников. Рёбра этих треугольников образуют четырёхугольник с проведённой в нём диагональю. Операция замены этой диагонали на другую называется flip (флип).

Из леммы 4 следует, что если ребро плохое, то флип сделает его хорошим.

Красное ребро — до флипа, зеленое — после

Лемма (5):

Флип плохого ребра уменьшает разность объёмов сферы и выпуклого многогранника, построенного на точках с заданными ребрами.

Доказательство:

[math]\triangleright[/math]

Рассмотрим два таких смежных треугольника, что ребро между ними является плохим.Четыре точки, принадлежащие смежным треугольникам, образуют тетраэдр. Проведём через какой-нибудь из двух треугольников плоскость. Вершина, противолежащая основанию тетраэдра, являющегося этим треугольником, лежит выше этой плоскости (так как для плохого ребра не выполняется локальный критерий Делоне), то есть тетраэдр не включается в объем фигуры. После флипа станет выполняться локальный критерий Делоне, то есть тело станет включать в себя тетраэдр. Поэтому после флипа плохого ребра объём тела увеличится на объём этого тетраэдра.

[math]\triangleleft[/math]

Лемма (6):

Флипами можно достичь хорошей триангуляции за конечное время.

Доказательство:

[math]\triangleright[/math]

Всего триангуляций заданного множества точек конечное число, и среди них есть триангуляция Делоне. Последовательность флипов плохих рёбер триангуляции образует такую последовательность триангуляций, что разность объёмов сферы и многогранника, постоенного по триангуляции убывает (по лемме 5). Эта последовательность конечна (при этом последней в последовательности является триангуляция Делоне), значит, число флипов, требуемых для достижения триангуляции Делоне, тоже конечно.

[math]\triangleleft[/math]

Лемма (7):

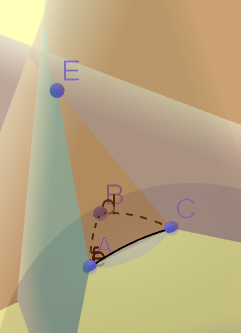
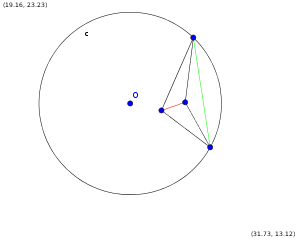
Если в триангуляцию Делоне вставить точку в некоторый треугольник и соединить его вершины с этой точкой, то получившиеся рёбра будут хорошими.

Доказательство:

[math]\triangleright[/math]

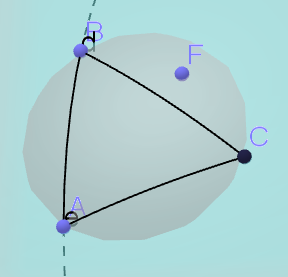
Пусть мы вставляем точку [math]P[/math]. Предположим, она была вставлена в треугольник [math]ABC[/math] не на ребро. Рассмотрим любое из рёбер — пусть это будет ребро [math]PC[/math]. Тогда проведем через точки [math]A[/math], [math]B[/math], [math]C[/math] плоскость [math]\alpha[/math], а так же проведем касательную плоскость [math]\beta[/math] к сфере через точку [math]C[/math]. Начнем уменьшать между этими плоскостями угол, двигая [math]\alpha[/math] к [math]\beta[/math]. В какой-то момент [math]\alpha[/math] пересечет точку [math]P[/math], а тогда мы предоставили плоскость, от которой все точки триангуляции находятся по одну сторону, так как изначально выше [math]\alpha[/math] была только точка [math]P[/math], а значит, ребро [math]PC[/math] удовлетворяет глобальному критерию Делоне. Аналогично для ребер [math]PA[/math] и [math]PB[/math]. Случай, когда точка вставляется на ребро, рассматривается аналогично.

[math]\triangleleft[/math]

Вставка точки

В обоих случаях для удобства реализации сначала добавим к триангуляции центр сферы.

Вставка точки, лежащей внутри триангуляции на поверхности сферы

Пусть мы добавляем точку [math]P'[/math]. Для начала локализуемся: поймём, в каком фейсе она лежит (или на каком ребре).

Если точка лежит внутри фейса, добавляем три ребра, сам фейс превращаем в один из новых смежных с вставляемой точкой и добавялем ещё два фейса.

Если же точка лежит на ребре, два смежных с ребром фейса превращаем в два новых, добавляем ещё два, а так же превращаем ребро, на которое вставляется точка, в ребро, которое заканчивается в этой точке, и вставляем три новых.

Итого у нас появилось несколько новых рёбер. Они все хорошие (по лемме 7), плохими могут оказаться только рёбра, противолежащие вставленной точке. Флипаем рёбра, пока триангуляция не станет хорошей.

Вставка точки, лежащей снаружи триангуляции на поверхности сферы

Пусть мы добавляем точку [math]P''[/math]. Нам нужно научиться вставлять точку в треугольник, одной из вершин которого является центр сферы. На самом деле, это теперь получится сделать естественным образом. Так как для локализации в треугольнике на поверхности сферы мы использовали предикат поворота относительно плоскости, проходящей через центр сферы и ребро, и вставляемой точки [math]P''[/math], то для проверки попадания в треугольник, содержащий центр сферы достаточно проверить, что точка [math]O[/math] видна из точки [math]P[/math], т.е. точка [math]P[/math] находится по определенную сторону от плоскости, проходящей через ребро и точку [math]O[/math], и противоположенная вершина для ребра является центром сферы.

Время работы

Лемма (8):

При вставке точки будут флипаться только рёбра, противолежащие вставленной точке.

Доказательство:

[math]\triangleright[/math]

Доказательство по индукции. База. По лемме 7 изначально не будут флипаться новые рёбра, инцидентные точке, то есть плохими могут оказаться только рёбра, противолежащие точке. Переход. Пусть мы вставили точку [math]P[/math]. Рассмотрим, что произойдёт с противолежащим ей ребром [math]AC[/math] после флипа, если оно плохое. До вставки точки [math]P[/math] для триангуляции выполнялся глобальный критерий Делоне, поэтому плоскость [math]\alpha[/math], проходящая через точки [math]A[/math], [math]C[/math] и [math]D[/math] содержала все точки по одну сторону от себя, теперь же по другую сторону еще будет только точка [math]P[/math]. Проведем плоскость [math]\beta[/math] через точки [math]P[/math] и [math]D[/math] так, что линия пересечения [math]\alpha[/math] и [math]\beta[/math] лежала бы в одной плоскости с касательной на сфере через точку [math]D[/math] к окружности, проходящей через точки [math]A[/math], [math]C[/math] и [math]D[/math]. Тогда уменьшая угол между этими плоскостями, двигая [math]\alpha[/math] к [math]\beta[/math], найдем момент, когда [math]\alpha[/math] пересечет точку [math]P[/math], а значит, в окружности, отсекаемой в этот момент плоскостью [math]\alpha[/math] не будет никаких точек. Значит, ребро [math]PD[/math] хорошее. Значит, после своего флипа ребро [math]AC[/math] уже не будет флипаться. Так как для рёбер [math]AP[/math] и [math]CP[/math] выполняется критерий Делоне, то плохими после флипа могут стать только рёбра [math]AD[/math] и [math]CD[/math] — то есть рёбра, противолежащие точке [math]P[/math].

[math]\triangleleft[/math]

Лемма (О степени вершины):

Математическое ожидание степени вершины после её вставки в триангуляцию Делоне равна [math]O(1)[/math].

Доказательство:

[math]\triangleright[/math]

Предположим, что мы вставляем [math]i+1[/math]-ую точку из последовательности из [math]n[/math] точек. Рассмотрим все перестановки из этих [math]i+1[/math] точек, означающие порядок вставки этих точек. Всего таких перестановок [math](i+1)![/math]. Тогда средняя степень последней вершины среди перестановок равна: [math]E(\operatorname{deg}(v_{i+1}))=\frac {\sum_{p=\operatorname{perm}(v_0, v_1, ..., v_i)} \operatorname{deg} (p[i+1])} {(i+1)!}[/math] Каждая из [math]i+1[/math] вершин побывает последней ровно [math]i![/math] раз, поэтому: [math]E(\operatorname{deg} (v_{i+1}))=\frac {\sum_{k=0}^{i} i! \operatorname{deg} (v_k)} {(i+1)!} = \frac {\sum_{k=0}^i \operatorname{deg}(v_k)} {i+1}[/math] По лемме о рукопожатиях [math]\sum_{k=0}^{i} \operatorname{deg}(v_k) = 2D[/math], где [math]D[/math] - количество ребер. Следовательно: [math]E(\operatorname{deg} (v_{i+1}))=\frac {2D} {i+1}[/math] Триангуляция Делоне на сфере является планарным графом на сфере, чья укладка эквивалентна укладке на плоскости. Значит, для неё справедлива формула Эйлера: [math]V-D+F=2[/math], где [math]V[/math] - количество вершин, а [math]F[/math] - количество граней. Так как каждая грань образована тремя рёбрами, и при этом при подсчёте каждое ребро учитывается дважды, имеем: [math]3F=2D=\gt F=\frac {2D} {3}[/math]. Подставив в формулу Эйлера, получим: [math]V-D+\frac {2D} {3}=2=\gt \frac {1} {3}D=V-2=\gt D=3(V-2)=3((i+1)-2)=3(i-1)[/math] В итоге [math]E(\operatorname{deg} (v_{i+1}))=\frac {2D} {i+1}=\frac {6(i-1)} {i+1}=O(1)[/math].

[math]\triangleleft[/math]

Теорема:

При вставке точки в триангуляцию Делоне на сфере в среднем придётся сделать [math]O(1)[/math] флипов.

Доказательство:

[math]\triangleright[/math]

Копирует случай на плоскости.

[math]\triangleleft[/math]

Удаление точки

В результате удаления у нас появляетя некоторый звездный многоугольник на сфере, который надо триангулировать. Из-за того, что у нас сфера, и задача триангуляции сведена к задаче построения выпуклой оболочки, то, следовательно, нам перестает быть важным критерий Делоне, нам просто нужно у звездного многоугольника на сфере как-то провести ребра так, чтобы было выпукло.

Представим себе, что вместо того, чтобы удалять точку, мы просто опускаем ее во внутрь до тех пор, пока она не перестает быть видимой в построенном на триангуляции многоугольнике. Предположим, что мы находимся в удаляемой точке, движемся в центр сферы и смотрим только в направлении движения.

Лемма (9):

Изначально нам будут видны грани, которые образуются внутри звездного многоугольника.

Доказательство:

[math]\triangleright[/math]

Исходный многогранник был выпуклым. Если бы мы могли видеть грани, находящиеся вне нашего звездного многоугольника, то это бы значило, что от удаляемой вершины до вершины, противолежащей ребру звездного многоугольника и лежащей в этой грани можно было бы провести ребро. Которого изначально не было.И это ребро лежало бы вне нашего многогранника, что противоречило бы его выпуклости.

[math]\triangleleft[/math]

Понятно, что мы постепенно перестаем видеть какие-то грани.Это происходит когда мы уходим ближе к центру, чем плоскость, соответствующая грани.

Теорема:

Когда мы перестаем видеть грани, они исчезают в порядке, соответствующем выделению их как ушей в новой триангуляции.

Доказательство:

[math]\triangleright[/math]

Расмотрим случай, когда у нас никакие четыре точки в звездном многоугольнике не лежат на одной окружности. Это значит, что все грани выпуклой оболочки будут треугольниками. Ухом является часть, которая по двум ребрам граничит с невидимыми гранями и по одному ребру может граничить с видимой. Посмотрим в каком порядке исчезают грани. Предположим нас есть кандидат на то, чтобы исчезнуть. Это какой-то выпуклый треугольник. Предположим, что у этого треугольника есть хотя бы два соседа, которые видны, но сам выпуклый многоугольник уже почти исчез (находится на одной плоскости с нашей точкой). Если мы видим две другие грани, то рассмотрим центры отрезков. рассмотрим [math]\varepsilon[/math]-окресности центров отрезков. Если мы точку спустим к центру сферы еще немного, то этот треугольник виден не будет, но [math]\varepsilon[/math]-окрестности будут видны две какие-то точки. Соединим их отрезком. Этот отрезок будет виден. Он не будет лежать на плоскости. Он не будет лежать под плоскостью. Тогла получается, что он лежит над плоскостью(ближе к краю сферы), значит, многогранник был невыпуклый. Получается, что грань ушла и у нее только один видимый сосед. Мы можем выделить грань как ухо. Общий случай, когда четыре точки в звездном многоугольнике могут лежать на одной окружности рассматривается аналогично. Теперь у нас возможна ситуация, когда перестает быть видимым не ухо, а грань, являющаяся выпуклым многоугольником(по лемме 2). Все хорошо, по лемме 3 мы можем триангулировать эту грань как угодно. Таким образом, мы будем перестраивать нашу выпуклую оболочку и, соответственно, триангуляцию.

[math]\triangleleft[/math]

Алгоритм удаления точки

1. Уберем точку.
2. Сделаем приоритетную очередь, в которой будем хранить пары отрезков, образующие ухо. Для этой очереди будем использовать предикат, сортирующий уши в порядке, в котором они пересекают луч по направлению от удаляемой точки к центру сферы.
3. На очередном шаге достаем ухо, отделяем его.
4. Добавляем в очередь получившиеся новые уши.

Предикат

[math]k = -\frac{\begin{vmatrix} A & 1 \\ B & 1 \\ C & 1 \\ P & 0 \end{vmatrix}}{\begin{vmatrix} A \\ B \\ C \end{vmatrix}}[/math]

[math]\begin{vmatrix} A & 1 \\ B & 1 \\ C & 1 \\ kP & 1 \end{vmatrix} + \begin{vmatrix} A \\ B \\ C \end{vmatrix} = 0 [/math]

[math]\begin{vmatrix} A & 1 \\ B & 1 \\ C & 1 \\ kP & 1 \end{vmatrix} + \begin{vmatrix} A \\ B \\ C \end{vmatrix} = \begin{vmatrix} a_x & a_y & a_z & 1 \\ b_x & b_y & b_z & 1 \\ c_x & c_y & c_z & 1 \\ kp_x & kp_y & kp_z & 1 \end{vmatrix} + \begin{vmatrix} a_x & a_y & a_z \\ b_x & b_y & b_z \\ c_x & c_y & c_z \end{vmatrix}[/math] [math] \Rightarrow [/math] [math]K\begin{vmatrix} A & 1 \\ B & 1 \\ C & 1 \\ P & 0 \end{vmatrix} + \begin{vmatrix} A \\ B \\ C \end{vmatrix} = 0[/math]

Время работы

Если наш звездный многоугольник состоит из [math]k[/math] точек, то на один запрос приоритетной очереди будет уходить [math] \mathcal{O}(\log(k)) [/math] операций. Значит общая ассимптотика будет [math] \mathcal{O}(k \log(k)) [/math].

Локализация в триангуляции

Построим алгоритм на сфере по аналогии с плоскостью.

Структура данных

Локализационная структура состоит из нескольких уровней, где каждый уровень — триангуляция Делоне. На нижнем уровне содержатся все точки. Далее точка с вероятностью [math] p [/math] попадает на следующий уровень. Если на последнем уровне находится одна точка, то дальше она уже не пойдет.

Лемма (О количестве уровней):

Математическое ожидание уровней в локализационной структуре [math] O(\log{n}) [/math].

Доказательство:

[math]\triangleright[/math]

То же самое, что и для плоскости.

[math]\triangleleft[/math]

Утверждение:

Локализационная структура занимает [math] O(n) [/math] памяти.

[math]\triangleright[/math]

Опять же доказательство копируется с плоскости.

[math]\triangleleft[/math]

Принадлежность треугольнику

Пусть даны точки [math]P[/math], [math]A[/math], [math]B[/math], [math]C[/math] на сфере с центром [math]O[/math], тогда [math]P[/math] принадлежит треугольнику [math]ABC[/math], тогда и только тогда, когда поворот [math]P[/math] относительно плоскостей [math]AOB[/math], [math]BOC[/math], [math]COA[/math] одинаковый.

Алгоритм

Чтобы найти треугольник, которому принадлежит точка запроса(точка [math]Q[/math]), сначала найдем ближайшую к ней точку триангуляции(точка [math]P[/math]), а зачем вдоль луча [math]PQ[/math] будем обходить треугольники, пока не локализуемся.

Поиск точки [math]P[/math]:

• На последнем уровне нашей структуры находиться [math]O(1)[/math] точек, поэтому просто переберем эти точки и найдем ближайшую к [math]Q[/math].
• При переходе с [math]i + 1[/math] уровня на [math]i[/math] новая ближайшая точка [math]V_i[/math] может быть только внутри окружности с центром в точке [math]Q[/math] проходящей через точку [math]V_{i + 1}[/math](ближайшая точка на [math]i + 1[/math] уровне). Переберем всех соседей точки [math]V_{i + 1}[/math] и выберем ближайшего к точке [math]Q[/math]. Повторяем эту операцию, пока можем приближаться к точке запроса.

Лемма (10):

Алгоритм найдет ближайшую точку

Доказательство:

[math]\triangleright[/math]

Допустим, что это не так. Это значит, что в внутри окружности с центром в точке [math]Q[/math], на которой лежит точка [math]P[/math], есть какие-то другие точки. То есть другими словами существует плоскость [math]\alpha[/math] проходящая через точку [math]P[/math], выше которой находятся точка [math]Q[/math](так как она центр) и какие-то точки триангуляции. Проведем в точке [math]P[/math] касательную плоскость [math]\beta[/math] к сфере. Очевидно, что она делит всё пространство на [math]2[/math] части: в первой нет никаких точек, а во второй находятся все точки триангуляции. Пусть между плоскостями [math]\alpha[/math] и [math]\beta[/math] угол [math]\gamma[/math]. Начнем его уменьшать, то есть поворачивать плоскость [math]\beta[/math]. Очевидно, что она начнет пересекать сферу, тогда она будет соответствовать какой-то окружности на сфере. При этом все точки сферы, которые выше плоскости [math]\beta[/math] будут выше плоскости [math]\alpha[/math], значит это будет вложенная окружность. Будем уменьшать угол [math]\gamma[/math] до того момента, когда какая-то точка [math]P'[/math], лежащая внутри окружности(такая есть по предположению), не станет принадлежать плоскости [math]\beta[/math]. В этот момент выше плоскости [math]\beta[/math] нет ни одной точки из триангуляции. Значит для ребра [math]PP'[/math] можно провести окружность, не содержащую других точек, то есть выполняется глобальный критерий Делоне. Значит в триангуляции должно быть ребро [math]PP'[/math], и по алгоритму мы должны были его перебрать и увидеть, что [math]P'[/math] ближе к точке [math]Q[/math] и перейти к ней. Получили противоречие, значит алгоритм правильно находит ближайшую точку.

[math]\triangleleft[/math]

Лемма (11):

Среднее число точек, лежащих внутри окружности с центром в точке [math]Q[/math] и проходящей через точку [math]V_{i + 1}[/math] равно [math]O(1)[/math].

Доказательство:

[math]\triangleright[/math]

Рассмотрим точки триангуляции [math]\{A_i\}[/math]. Для каждой точки [math] A_i[/math] проведем окружность с центром в ней, проходящую через ближайшую к ней точку. Посчитаем во сколько окружностей в среднем попадет точка какая-то точка [math]U[/math]. Проведем через [math]OU[/math] три плоскости так, чтобы они делили всё пространство на [math]6[/math] равных частей. Покажем, что в одной части [math]O(1)[/math] окружностей будут включать в себя точку [math]U[/math], тогда всего таких окружностей будет тоже [math]O(1)[/math]. Рассмотрим одну часть. Отсортируем точки, которые ей принадлежат, по степени удаленности от точки [math]U[/math]. Окрасим точки в два цвета: красный — точки с [math]i[/math] уровня черный — точки с [math]i + 1[/math] уровня Если на [math]j[/math]-ой позиции находится черная точка, то точки с индексом [math]j + 1[/math] и далее не будут содержать в окружности точку [math]U[/math](потому что [math]j[/math] была ближайшей на предыдущем уровне из этой части пространства). Тогда если [math] X [/math] — количество окружностей, которым принадлежит точка [math]U[/math], то так как точка проходит на следующий уровень с вероятностью [math]p[/math]: [math]E(X) \leqslant \sum_{i = 1}^{\infty}{i \cdot p(1 - p) ^ i} =[/math] [math]\sum_{i = 1}^{\infty}{\sum_{j = i}^{\infty}{p (1 - p) ^ j}} =[/math] [math]p\sum_{i = 1}^{\infty}{(1-p)^i \cdot (\sum_{j = 0}^{\infty}{(1 - p) ^ j})} = \sum_{i = 1}^{\infty}{(1-p)^i} = \dfrac{1-p}{p} = O(1)[/math] Получается, что каждая точка принадлежит [math]O(1)[/math], следовательно внутри каждой окружности содержит [math]O(1)[/math] точек.

[math]\triangleleft[/math]

Лемма (12):

Средняя степень точек на [math]i[/math] уровне внутри окружности с центром в точке [math]Q[/math] и проходящей через точку [math]P_{i + 1}[/math](ближайшая точка на [math]i + 1[/math] уровне)

Доказательство:

[math]\triangleright[/math]

Пусть есть функция [math]circle(q, p, i)[/math], возвращающая [math]1[/math], если точка [math]p[/math] принадлежит окружности с центром в точке [math]q[/math], проходящую через ближайшую к [math]q[/math] на [math]i[/math] уровне точку, а иначе [math]0[/math]. Пусть [math]Points_i[/math] — множество точек на [math]i[/math]-ом уровне. [math]X[/math] — степень вершины внутри окружности, тогда: [math]E(X) = \dfrac{\sum\limits_{q \in Points_{i - 1}}{\sum\limits_{p \in Points_{i - 1}}{circle(q, p, i) \cdot deg(p)}}}{\left| Points_{i - 1} \right|} =[/math] Меняем порядок суммирования, и получаем: [math]= \dfrac{\sum\limits_{p \in Points_{i - 1}}{deg(p) \sum\limits_{q \in Points_{i - 1}}{circle(q, p, i)}}}{\left| Points_{i - 1} \right|} \leqslant[/math] По предыдущей лемме получаем: [math]\leqslant \dfrac{\sum\limits_{p \in Points_{i - 1}}{deg(p) \sum\limits_{1 \dots \infty}{i \cdot p \cdot (1 - p) ^ i}}}{\left| Points_{i - 1} \right|} \approx[/math] [math]\approx \dfrac{\sum\limits_{p \in Points_{i - 1}}{deg(p)}}{\left| Points_{i - 1} \right|} = \dfrac{O(n)}{n} = O(1)[/math]

[math]\triangleleft[/math]

Лемма (13):

Один уровень в среднем обрабатывается за [math]O(1)[/math]

Доказательство:

[math]\triangleright[/math]

По лемме 11 алгоритм пройдет в среднем [math]O(1)[/math] вершин, степень которых так же равна по лемме 12 [math]O(1)[/math], следовательно один уровень будет обработан за [math]O(1)[/math].

[math]\triangleleft[/math]

Лемма:

Точка на сфере может быть ближайшей для не более [math]6[/math] точек.

Доказательство:

[math]\triangleright[/math]

Пусть это не так. Тогда некоторая точка [math]P[/math] является ближайшей для [math]7[/math] точек: [math]A_1 \dots A_7[/math]. Проведем отрезки [math]O A_i[/math]. Получили семигранный угол. По свойствам многогранных углов: сумма их плоских углов не превосходит [math]360[/math]. Проведем [math]7[/math] полуплоскостей с основанием [math]OP[/math], каждая из которых содержит соответствующий отрезок [math]O A_i[/math]. Плоский угол [math]A_i O A_{i + 1}[/math] не меньше угла между полуплоскостями, содержащими отрезки [math]O A_i[/math] и [math]O A_{i + 1}[/math]. Тогда так как сумма углов между полуплоскостями равна [math]360[/math], получаем, что сумма плоских углов в семигранном угле не менее [math]360[/math]. Противоречие, значит такого быть не может.

[math]\triangleleft[/math]

Лемма:

Степень ближайшей вершины [math]O(1)[/math]

Доказательство:

[math]\triangleright[/math]

Доказательство копирует случай на плоскости.

[math]\triangleleft[/math]

Лемма:

На втором этапе алгоритма луч в среднем пересечет [math]O(1)[/math] ребер.

Доказательство:

[math]\triangleright[/math]

Рассмотрим окружность с центром в точке [math]Q[/math], проходящую через ближайшую для неё точку триангуляции [math]P_{i + 1}[/math]. Количество таких ребер, хотя бы одна граница которых принадлежит окружности не превосходит суммы степеней вершин внутри окружности, следовательно их [math]O(1)[/math]. Осталось посчитать ребра, границы которых не лежат внутри окружности. При вставке точки [math]Q[/math] в триангуляцию для таких ребер испортится критерий Делоне, так как внутри любой окружности построенной на этом ребре будет либо точка [math]Q[/math], либо точка [math]P_{i + 1}[/math]. Значит, что эти ребра надо будет флипнуть, а так как при вставке в среднем флипается [math]O(1)[/math] ребер, то луч пересечет [math]O(1)[/math] ребер.

[math]\triangleleft[/math]

Теорема (Следствие):

Локализация в среднем работает за [math]O(\log{n})[/math]

Движение вдоль луча

Когда нам надо пройти по триангуляции вдоль какого-то луча [math]PQ[/math], то ,оказавшись в каком-то треугольнике, надо проверить, что точка [math]Q[/math] принадележит этому треугольнику. Если принадлежит, то мы останавливаем свой обход, иначе находим какую сторону пересекал луч и переходим в смежный этой стороне треугольник.

Теорема:

Луч [math]PQ[/math] пересекает отрезок [math]AB[/math] тогда и только тогда, когда повороты точек [math]A[/math] и [math]B[/math] относительно [math]PQ[/math] различены, а повороты [math]B[/math] и [math]Q[/math] относительно [math]AP[/math] совпадают.

Доказательство:

[math]\triangleright[/math]

Необходимость [math]AB[/math] пересекает [math]PQ[/math]. Очевидно, что в этом случае повороты точек [math]A[/math] и [math]B[/math] относительно [math]PQ[/math] различены. Рассмотрим повороты [math]B[/math] и [math]Q[/math] относительно [math]AP[/math]. Если они различны, тогда луч [math]PQ[/math] и отрезок [math]AB[/math] лежат в разных полусферах, но они пересекаются, значит такого быть не может и повороты должны совпадать. Достаточность Предикат выполняется. Значит отрезок [math]AB[/math] пересекает прямую [math]PQ[/math]. Луч [math]PQ[/math] в свою очередь есть половина прямой [math]PQ[/math]. Из того, что повороты [math]B[/math] и [math]Q[/math] относительно [math]AP[/math] совпадают, следует, что отрезок [math]AB[/math] находится в одной полусфере с лучем [math]PQ[/math], значит они пересекаются.

[math]\triangleleft[/math]