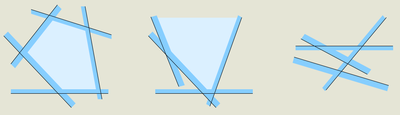
Пересечение полуплоскостей, связь с выпуклыми оболочками
Задача: есть конечное множество полуплоскостей, найти фигуру их пересечения или сообщить что оно пусто.
Для начала заметим, что если пересечение не пусто, то оно выпукло. (Доказательство — Пересечение выпуклых фигур выпукло, а полуплоскость выпукла)
Пусть полуплоскости заданы уравнениями прямых и ориентацией, с какой стороны от прямой лежит полуплоскость.
Сначала рассмотрим все полуплоскости, которые "смотрят", то есть ориентированны, вниз. Аналогично можно рассмотреть все полуплоскости, которые ориентированны вверх.
| Лемма: |
| Доказательство: |
|
Для проверки предиката нужно определить знак выражения , где — точка пересечения прямых и . Эта точка находится из уравнения . Решением будет . Подставим это решение в и домножим на определитель. |
Таким образом, если представить прямую как точку с однородными координатами , то этот предикат — всего лишь поворот, а проверка предиката — проверка очередной точки в обходе Грэхема для нахождения выпуклой оболочки.
Алгоритм:
- Отсортировать все полуплоскости по углу наклона;
- Запустить обход Грэхема для полуплоскостей, смотрящих вниз (с предикатом-определителем);
- Запустить обход Грэхема для полуплоскостей, смотрящих вверх;
- Пересечь две цепочки.
От пересечения цепочек напрямую зависит фигура пересечения: неограниченная область получается если одна из цепочек пуста, а ограниченная — когда обе цепочки не пусты и пересекаются.
Связь пересечения полуплоскостей с выпуклой оболочкой
| Лемма: |
Пересечение полуплоскостей может быть получено построением выпуклой оболочки в двойственном прострастве для множества точек, являющихся дуальным преобразованием исходных полуплоскостей |
| Доказательство: |
|
Важно: Покажем конструктивный алгоритм для множестве полуплоскостей, не содержащих вертикальный полуплоскости. После леммы приведены два рассуждения, позволяющие снять данное ограничение. Рассмотрим планарный случай и предположим, что вертикальные и параллельные прямые отсутствуют (в конце приведем два способа решения данной проблемы). Пусть у нас есть множество ориентированных прямых, каждая из которых задает полуплоскость(направление вектора нормали задаёт нужную полуплоскость). Тогда каждую плоскость мы можем превратить в точку в двойственном пространстве: . Далее воспользуемся основными свойствами дуальной трансформации (см. доказательтсво в конспекте о двойственном прострастве):
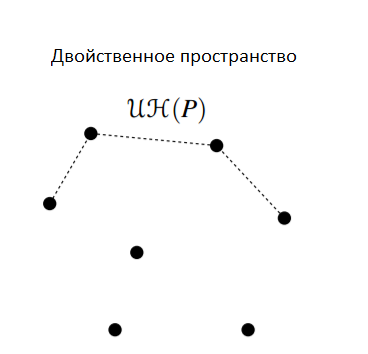
Рассмотрим множество точек() в двойственном пространстве и рассмотрим верхнюю часть выпуклой оболочки, построенной на этих точках. Обозначим её за (Upper hull). По свойству выпуклой оболочки, любое ребро из цепи содержит "ниже" себя все точки множества , а так же эта цепь соединяет самую правую точку с самой левой. Рассмотрим какую-то точку и заметим, что она будет принадлежать цепи прямая : и все точки из лежат ниже (сейчаc мы жили в двойственном пространстве). В обычном пространстве данный факт эквивалентен следующему:
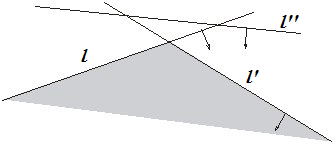
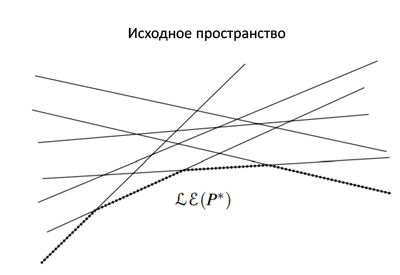
Итого: у нас есть точка на прямой , лежащая ниже всех остальных прямых из . Взглянем на планарный граф множества(рис.2) прямых. Из факта выше, мы можем понять, что внесла ребро, которая принадлежит нижней части планарного графа(именно той, что задаёт часть пересечения полуплоскостей). Вернемся к и заметим, что при обходе цепи, координата точек Х растет. Если же мы будет обходить цепочку из , образующую пересечение полуплоскостей, мы заметим, что наклон прямых уменьшается. Учитывая этот факт, и то что наклон линии совпадет с X координатой точки(вспоминаем отображение и применяем производную), можно сделать вывод, что обход слева направо точек из цепи , совпадает с обходом точек из справа налево. |