Теорема Холла

Определения

Пусть [math]G(V,E)[/math] — двудольный граф. [math]L[/math] — множество вершин левой доли. [math]R[/math] — множество вершин правой доли.

Определение:

Полным (совершенным) паросочетанием (англ. perfect matching) называется паросочетание, в которое входят все вершины.

Определение:

Пусть [math]X \subset V [/math]. Множeство соседей [math]X[/math] (англ. neighborhood) определим формулой: [math]N(X)= \{ y \in V \mid (x,y) \in E , x \in X\}[/math]

Теорема

Теорема (Холл ):

Полное паросочетание существует тогда и только тогда, когда для любого [math]A \subset L [/math] выполнено [math]|A| \leqslant |N(A)|[/math].

Доказательство:

[math]\triangleright[/math]

[math]\Rightarrow[/math] Очевидно, что если существует полное паросочетание, то для любого [math]A \subset L [/math] выполнено [math]|A| \leqslant |N(A)|[/math]. У любого подмножества вершин есть по крайней мере столько же соседей (соседи по паросочетанию). [math]\Leftarrow[/math] В обратную сторону докажем по индукции (будем добавлять в изначально пустое паросочетание [math]P[/math] по одному ребру и доказывать, что мы можем это сделать, если [math]P[/math] не полное). Таким образом, в конце получим что [math]P[/math] — полное паросочетание. База индукции Вершина из [math]L[/math] соединена хотя бы с одной вершиной из [math]R[/math]. Следовательно база верна. Индукционный переход Пусть после [math]k\lt n[/math] шагов построено паросочетание [math]P[/math]. Докажем, что в [math]P[/math] можно добавить вершину [math]x[/math] из [math]L[/math], не насыщенную паросочетанием [math]P[/math]. Рассмотрим множество вершин [math]H[/math] — все вершины, достижимые из [math]x[/math], если можно ходить из [math]R[/math] в [math]L[/math] только по ребрам из [math]P[/math], а из [math]L[/math] в [math]R[/math] по любым ребрам из [math]G[/math]. Тогда в [math]H[/math] найдется вершина [math]y[/math] из [math]R[/math], не насыщенная паросочетанием [math]P[/math], иначе, если рассмотреть вершины [math]H_L[/math] (вершины из [math]H[/math] принадлежащие [math]L[/math]), то для них не будет выполнено условие: [math]|H_L| \leqslant |N(H_L)|[/math]. Тогда существует путь из [math]x[/math] в [math]y[/math], который будет удлиняющим для паросочетания [math]P[/math] (т.к из [math]R[/math] в [math]L[/math] мы проходили по ребрам паросочетания [math]P[/math]). Увеличив паросочетание [math]P[/math] вдоль этого пути, получаем искомое паросочетание. Следовательно предположение индукции верно.

[math]\triangleleft[/math]

Пояснения к доказательству

Пример

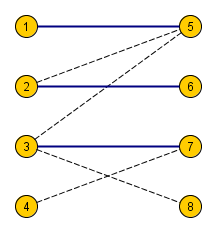
Пусть было построено паросочетание размером [math]3[/math] (синие ребра).

Добавляем вершину с номером [math]4[/math].

Во множество [math]H[/math] вошли вершины с номерами [math]1[/math], [math]3[/math], [math]4[/math], [math]5[/math], [math]7[/math], [math]8[/math].

Ненасыщенная вершина из правой доли всегда найдется (в примере вершина с номером [math]8[/math]), т.к иначе получаем противоречие:

1. В [math]H_R[/math] входят только насыщенные вершины.
2. [math]N(H_L) = H_R[/math]
3. В [math]H_L[/math] по крайней мере [math]H_R+1[/math] вершин (соседи по паросочетанию для каждой вершины из [math]H_R[/math] и ещё одна вершина, которую пытаемся добавить).

Цепь [math]{4, 7, 3, 8}[/math] является удлиняющей для текущего паросочетания.

Увеличив текущее парасочетание вдоль этой цепи, мы насытим вершину с номером [math]4[/math].

Источники информации

• Википедия — Теорема Холла
• Wikipedia — Hall's marriage theorem