Суффиксный массив

Определение:

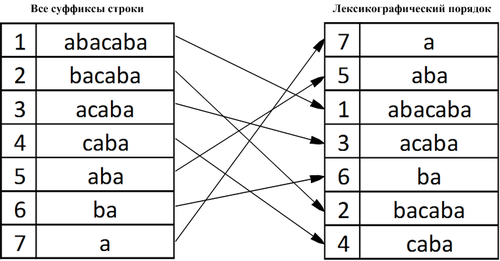
Cуффиксным массивом (англ. suffix array) строки [math]s[1 .. n][/math] называется массив [math]suf[/math] целых чисел от [math]1[/math] до [math]n[/math], такой, что суффикс [math]s[suf[i]..n][/math] — [math]i[/math]-й в лексикографическом порядке среди всех непустых суффиксов строки [math]s[/math].

Пример

[math]s = abacaba[/math]

Значит, суффиксный массив для строки [math]s[/math] равен [math][7, 5, 1, 3, 6, 2, 4][/math].

Восстановление строки по суффиксному массиву

Задача:

Дан суффиксный массив некоторой строки [math]s[/math], необходимо восстановить строку за время [math]O(|s|)[/math].

Вариант для бесконечного алфавита

Так как наш алфавит не ограничен, можно [math]i[/math]-й в лексикографическом порядке суффикс сопоставить с [math]i[/math]-й буквой в алфавите.

Доказательство корректности

Если отсортировать суффиксы, то первые буквы будут расположены в том же порядке, как и в алфавите.

Псевдокод

string fromSuffixArrayToString(int[] sa):
  for i = 1 to n
       s[sa[i]] = alphabet[i] 
  return s

Вариант для минимально возможного

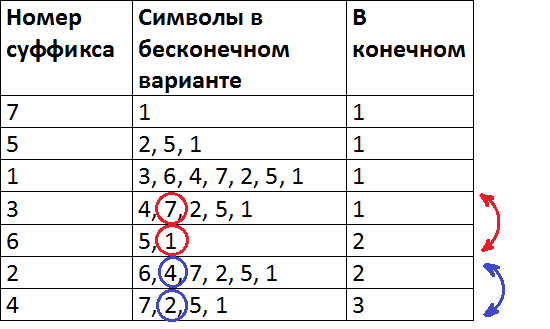
Для начала вместо каждого символа строки поставим символ из бесконечного алфавита в промежуточную строку [math]tmp[/math], как в решении выше. Пусть, мы рассматриваем [math]i[/math]-й в лексикографическом порядке суффикс (т.е. и [math]i[/math]-й символ строки). Его первый символ будет равен первому символу предущего в лексикографическом порядке суффикса, если [math]tmp[sa[i - 1] + 1] \lt tmp[sa[i] + 1][/math], т.е. и их строки без первого символа так же в лексикографическом порядке. Иначе он должен быть больше, т.к. рассматриваемый суффикс следующий в лексикографическом порядке.

Пример

Дан суффиксный массив [math][7, 5, 1, 3, 6, 2, 4][/math]. Цветами показаны места, после которых добавляются новые символы.

Псевдокод

string fromSuffixArrayToString(int[] sa):
  for i = 1 to n
       tmp[sa[i]] = alphabet[i]
  cur = 1
  s[1] = alphabet[1]
  for i = 2 to n
       j = sa[i - 1]
       k = sa[i]
       if tmp[j + 1] > tmp[k + 1] 
           cur++
       s[i] = alphabet[cur]       
  return s

Доказательство минимальности

Докажем от противного. Пусть, есть решение в котором использовано меньше букв. Тогда найдется позиция в которой, наше решение отличается от минимального, причем в минимальном остается та же буква, как в предыдущем суффиксе, а в нашем появляется новая. Рассмотрим эти два подряд идущих суффикса. В решении выше добавится новая буква, только если продолжение первого суффикса лексикографически больше, чем продолжение второго. Получается, что в минимальном решении первый суффикс лексикографически больше, чем второй, что неверно. Пришли к противоречию.

Применения

Число различных подстрок в строке

Вычисление числа различных подстрок в строке за время [math]O(|s| \log(|s|))[/math] и [math]O(|s|)[/math] дополнительной памяти с использованием LCP.

Максимальная по длине ветвящаяся влево и вправо строка

Данная задача также может быть решена при помощи суффиксного дерева.

Самая длинная строка p, входящая в t дважды и не пересекаясь

Задача:

Поиск самой длинной строки [math]p[/math], входящей в строку [math]t[/math] дважды и не пересекаясь.

Основные положения

Построим суффиксный массив строки [math]t[/math] и посчитаем на нем LCP. Для суффикса [math]s[/math] символом [math]s'[/math] будем обозначать индекс этого суффикса в суффиксном массиве.

Рассмотрим какие-нибудь суффиксы [math]i[/math] и [math]j[/math] строки [math]t[/math] такие, что [math]i' \leqslant j'[/math]. Будем говорить, что строка [math]s[/math] соответствует каким-нибудь суффиксам [math]i[/math] и [math]j[/math], если она равна максимальному префиксу этих суффиксов. Будем говорить, что суффиксы [math]i[/math] и [math]j[/math] соответствуют строке [math]s[/math], если [math]s[/math] входит в [math]t[/math] дважды и не пересекаясь, а суффиксы [math]i[/math] и [math]j[/math] соответствуют позициям этих вхождений.

Для произвольной строки [math]s[/math] и двух суффиксов, соответствующих ей, введем два условия:

1. [math]\max(|i|, |j|) \geqslant \min(|i|, |j|) + |s|[/math]
2. [math]|s| = \min\limits_{k=i'\dots j'}lcp[k][/math]

Утверждение:

Строка [math]s[/math] входит в [math]t[/math] дважды и не пересекаясь тогда и только тогда, когда она удовлетворяет условию 1.

[math]\triangleright[/math]

Необходимое условие: Если строка [math]s[/math] входит в [math]t[/math] дважды и не пересекаясь, то один из суффиксов [math]i[/math] и [math]j[/math] хотя бы на [math]|s|[/math] длиннее другого. Т.е. условие 1 выполнено. Достаточное условие: Из того, что выполняется условие 1 следует, что один из суффиксов хотя бы на [math]|s|[/math] длиннее другого. При этом они оба начинаются со строки [math]s[/math]. Поэтому строка [math]s[/math] входит в [math]t[/math] дважды и не пересекаясь.

[math]\triangleleft[/math]

Утверждение:

Если строка [math]s[/math] является максимальной входящей в [math]t[/math] дважды, то она удовлетворяет условию 2.

[math]\triangleright[/math]

Пусть это не так и [math]|s| \lt \min\limits_{k=i'\dots j'}lcp[k][/math] (больше она быть не может). Тогда получим, что [math]|s|[/math] меньше, чем длина наибольшего общего префикса суффиксов [math]i[/math] и [math]j[/math], чего быть не может по построению [math]i[/math] и [math]j[/math].

[math]\triangleleft[/math]

Наивный алгоритм

1. Построим суффиксный массив, посчитаем на нём LCP.
2. Переберем все пары [math]i[/math] и [math]j[/math] такие, что они удовлетворяют условиям 1 и 2 и возьмем среди них максимум по длине строки.

Этот алгоритм можно реализовать за [math]O(n^3 + \mathrm{SA})[/math] или за [math]O(n^2 + \mathrm{SA})[/math], где [math]\mathrm{SA}[/math] — время построения суффиксного массива.

Оптимальное решение

Идея

Будем перебирать всевозможные подстроки [math]s[/math] строки [math]t[/math] такие, что они входят в [math]t[/math] дважды и удовлетворяют условию 2 при любых [math]i[/math] и [math]j[/math], где [math]i[/math] и [math]j[/math] — суффиксы, соответствующие двум любым вхождениям [math]s[/math] в [math]t[/math] (т.е. не обязательно непересекающимся). Для каждой такой строки [math]s[/math] попробуем найти [math]i[/math] и [math]j[/math], удовлетворяющие условию 1. Таким образом, мы рассмотрим все строки, соответствующие условиям 1 и 2, и, следовательно, найдем ответ. Алгоритм корректный.

Заметим теперь, что искомые строки [math]s[/math] — это префиксы суффиксов [math]k[/math] длины [math]lcp[k][/math]. Для того, чтобы найти для каждой такой строки [math]s[/math] суффиксы [math]i[/math] и [math]j[/math], удовлетворяющие условию 1, воспользуемся стеком.

Алгоритм

1. Будем идти по суффиксному массиву в порядке лексикографической сортировки суффиксов. В стеке будем хранить префиксы уже рассмотренных суффиксов [math]k[/math] длины [math]lcp[k'][/math] (т.е. строки [math]s[/math]) в порядке увеличения длины. Для каждой строки из стека также будем хранить минимальный по длине суффикс [math]i[/math] и максимальный по длине [math]j[/math]. Обозначим за [math]st[/math] вершину стека, а за [math]s[/math] — текущий рассматриваемый суффикс.
2. Возможны три случая:
   • [math]|st| = lcp[s'][/math]
     Тогда просто обновляем [math]i[/math] и [math]j[/math] для вершины стека.
   • [math]|st| \geqslant lcp[s'][/math]
     В этом случае добавляем новую вершину в стек и обновляем для неё [math]i[/math] и [math]j[/math].
   • [math]|st| \leqslant lcp[s'][/math]
     Достаем вершину из стека и пробрасываем значения [math]i[/math] и [math]j[/math] из неё в новую вершину стека. Это нужно для того, чтобы не потерять значения [math]i[/math] и [math]j[/math], которые были посчитаны для строк большей длины, но так же актуальны для строк меньшей длины.
3. Если в какой-то момент [math]i[/math] и [math]j[/math] станут удовлетворять условию 1, обновляем ответ.

Оценка времени работы

Т.к. подсчёт [math]lcp[/math] выполняется за [math]O(n)[/math], и для каждого суффикса мы выполняем [math]O(1)[/math] операций, то итоговое время работы [math]O(n + \mathrm{SA})[/math], где [math]\mathrm{SA}[/math] — время построения суффиксного массива.

См. также

• Построение суффиксного массива с помощью стандартных методов сортировки
• Алгоритм поиска подстроки в строке с помощью суффиксного массива
• Алгоритм Касаи и др.

Источники

• Дэн Гасфилд — Строки, деревья и последовательности в алгоритмах: Информатика и вычислительная биология — СПб.: Невский Диалект; БХВ-Петербург, 2003. — 654 с: ил.
• MAXimal :: algo :: Суффиксный массив
• Википедия — Суффиксный массив
• Wikipedia — Suffix array
• Habrahabr — Суффиксный массив — удобная замена суффиксного дерева