Конструирование комбинаторных объектов и их подсчёт
Версия от 14:42, 24 декабря 2017; Mervap (обсуждение | вклад) (Новая страница: «==Последовательности== {{Утверждение |statement= Пусть <tex>A=\{a_{1},a_{2}, \ldots ,a_{n}\}</tex> {{---}} множество ...»)
Содержание
Последовательности
| Утверждение: |
Пусть — множество из различных объектов, — множество всех последовательностей из элементов , — количество объектов веса . Тогда количество последовательностей веса можно вычислить как . |
Подсчет битовых векторов длины
Пусть , , — множество всех битовых векторов. Тогда .
Подсчет последовательностей из маленьких и больших элементов
Пусть , , — множество всех последовательностей из маленьких и больших элементов . Тогда , где — -ое число Фибоначчи [1].
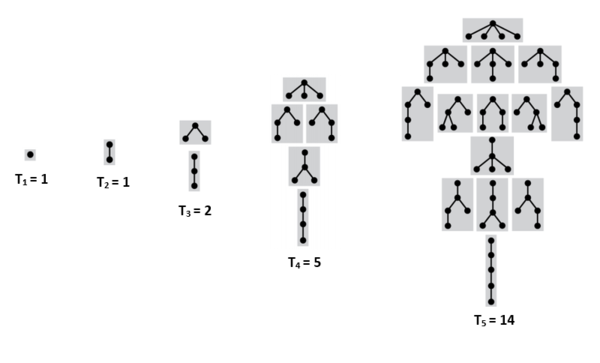
Подсчет подвешенных непомеченных деревьев с порядком на детях
Пусть — количество деревьев с вершинами, . — множество всех последовательностей из деревьев. — количество последовательностей с суммарным количество вершин . Чтобы получить дерево из вершин достаточно взять вершину и подвесить к ней последовательность деревьев с суммарным количеством вершин . Тогда , где — -ое число Каталана, а .
Множества
| Утверждение: |
Пусть — множество из различных объектов, — множество всех множеств объектов, составленных из элементов , — количество объектов веса , составленных из элементов , . Тогда количество множеств из объектов суммарного веса можно вычислить как , где — количество таких множеств, что они содержат объекты суммарного веса . |
Количество множеств из элементов или
Пусть , — множество всех множеств из , , . Тогда , где
Количество разбиений на слагаемые
Пусть , — множество всех разбиений на слагаемые, , . Тогда , где , что, как не сложно заметить, соответсвует формуле, полученной методом динамического программирования.